Hello Codeforces. Today I'm writing about a Math topic that is simple, but resources and problems are limited.
SLAE stands for system of linear equations. Basically, consider we have a set of equations of the form :
a0·x0 + a1·x1 + a2·x2 + ... + an - 1·xn = val0
b0·x0 + b1·x1 + b2·x2 + .... + bn - 1·xn - 1 = val1
c0·x0 + c1·x1 + c2·x2 + .... + cn - 1·xn - 1 = val2
.....
Note that all a, b, c... are real-valued arrays and all vali are arbitrary reals. Realize how x0, x1, ...xn - 1 appear in each of the equations. In the post below, it is assumed we are dealing with Rationals, and not only integers.
Now, we want to find values of [x0, x1...xn - 1] that satisfy each of the given equations listed, given all a, b, c... and vali. The simplest method to find such solutions is to use Gaussian Elimination, that solves the problem in O(N3), where N = number of equations = number of variables .
To Learn about Gaussian Elimination, click here. Today, we shall learn about 2 special class of problems that can be solved using Gaussian Elimination.
Problem 1 : Markov Chains and Cyclic Expected Values :
Many a times as a part of expected value problems, you are expected to sum up infinite series that hold as limits, as probabilities lie in the closed interval [0, 1]. For example,
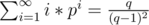 , as
, as 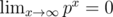
However, not always can we expect the variables whose Expected value we need to calculate to be independent. Consider you have N random variables 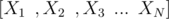 , where , there are cyclic dependencies among the variables for their expected values, i.e consider E(X1) depends on E(X2), E(X2) on E(X3) and E(X3) depends on E(X1). So, there exists an infinite loop for calculating the Expected values of the random variables.
, where , there are cyclic dependencies among the variables for their expected values, i.e consider E(X1) depends on E(X2), E(X2) on E(X3) and E(X3) depends on E(X1). So, there exists an infinite loop for calculating the Expected values of the random variables.
For example, consider the following problem :
You are given Tree T consisting of N nodes. Initially there is a player in node S. In a single move, he moves to one of the adjacent nodes of the node he is currently at, each with equal probability. What is the expected number of moves before he reaches node T ?.
Here, we need to understand that the probabilities are infinite as well as cyclic. Creating a simple formula for the answer is quite hard. The Expected value starting from node S depends on some neighbor of node S, however, the Expected value of some neighbor of node S depends on Expected value of node S. Notice that whenever we reach a particular node, the probability of moving to any other node regardless of the number of steps performed always remains the same. So, this is a Markov Chain. Let's consider the transition matrix of this chain.
Create a matrix P, where P[i][j]= probability of moving from node i to j in a single move. Now, Let E(i) denote the expected number of steps needed to reach node T from node i.
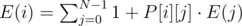 .
.
Try and take a moment and think about why this formula is correct.
Surprise Surprise, this can be modeled as SLAE. Rewrite equations as :
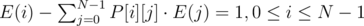 . So the system is :
. So the system is :
\begin{equation} \begin{pmatrix} 1-P[0][0] & -P[0][1] & ... & -P[0][N-1] \newline -P[1][0] & 1-P[1][1] & ... & -P[1][N-1] \newline .... \newline -P[N-1][0] & -P[N-1][1] & ... & 1-P[N-1][N-1] \end{pmatrix} \cdot \begin{pmatrix} E(0) \newline E(1) \newline . \newline . \newline E(n-1) \end{pmatrix} = \begin{pmatrix} 1 \newline 1 \newline .. \newline 1 \end{pmatrix} \end{equation}
This is the equation (IN - P)·E = 1, We need to find E. Note that for node T, we need to have P[t][i] = 0, t ≠ i and P[t][t] = 1, as we won't move from node T, it is an absorbent state of the Markov chain. So, the Tth row of matrix IN - P will be all zeros. Also, the equation does not hold true for node T. Also, we know E(t) = 0. So, the part P[i][t]·E(t) does not affect any of the equations. So, just remove the Tth row and column from both sides of the equation.
The matrix is now a square (N - 1)·(N - 1) matrix, that is invertible. Invert the matrix using Gaussian Elimination augmenting with the RHS, to obtain E, i.e. E(i), 0 ≤ i ≤ N - 1, i ≠ T
We can use this generic technique in all cases where the expected values are cyclic in nature , i.e expected value of state A depends on state B, and expected value of state B depends on state A. We can use any prime mod too, to obtain expected value in Modulo. Just remember : dependent random variables A - > B, B - > A : Gaussian Elimination .
Practice Problems :
One (Same problem as above) My Code
Problem 2 : Xor's using SLAE
Pr-requisite : Vector Space properties, Linear Algebra.
Without reading the link, proceed at your own risk.
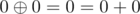 mod 2
mod 2
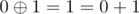 mod 2
mod 2
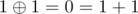 mod 2
mod 2
So, xor is just bit-wise addition mod 2. We can represent the xor of two integer's x, y as vector addition in  . For example ,
. For example ,
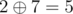 i.e. ,
i.e. ,
\begin{equation} \begin{pmatrix} 0 \newline 1 \newline 0 \end{pmatrix} + \begin{pmatrix} 1 \newline 1 \newline 1 \end{pmatrix} \equiv \begin{pmatrix} 1 \newline 0 \newline 1 \end{pmatrix}
Mod \space 2
\end{equation}
So, we can use this addition to replace xor.The main advantage of this scheme is that we have converted the subset xor problem to solving a linear system instead. Consider we want to find a, b, c such that:
a·v1 + b·v2 + c·v3 ≡ x Mod 2, given v1, v2, v3 and x. Here v1, v2, v3, x are arbitrary binary column vectors. This is equivalent to solving the linear system :
\begin{equation} \begin{pmatrix} v1 & v2 & v3 \end{pmatrix} \cdot \begin{pmatrix} a \newline b \newline c \end{pmatrix} \equiv x \hspace{0.2cm} Mod \hspace{0.2cm} 2 \end{equation}.
Since a, b, c can only belong to {0, 1}, this is precisely finding a solution to subset xor.
Note that the span of any given set of size N is a vector space. There is a concept called as Basis of a vector space , i.e a smallest size subset of a given set that spans the entire vector space spanned by the original set given. We can solve the same problem over smaller sized basis rather than using all the elements of the set.
Via the Basis, we can solve useful xor based problems such as :
1> Given a set S of size N, find the number of distinct integers that can be represented using xor over the set of the given elements.
2> How many subsequences of a given set S of size N have xor equal to X. (Do it yourself).
3> What is the maximum possible xor you can have using a subset of a given set :
All of these problems can be modeled using SLAE in Mod 2. We can do operations faster in Mod 2 using bitset having complexity 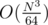 .
.
Problems :






