Catalan Numbers is a well known sequence of integers that appear in combinatorics, there is a chance that you might have run into such counting problems and you might have even solved them with DP without realizing that they are a known sequence. Here are a fewis a problems to get us started.↵
↵
### Binary Trees Count↵
↵
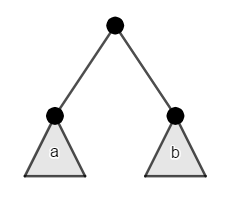
Find the count of different binary trees with $n$ nodes, we'll denote to that by $C_n$. This can be solved by observing the substructure of the problem: ↵
↵
↵
↵
From the root, the left subtree $a$ can be _any_ binary tree of size $x$, the right subtree $b$ can be _any_ binary tree of size $y$, such that $x+y=n-1$ (as we took one node as the root). With the base case at $C_0=1$ as the empty tree is a valid tree of size $0$. This directly gives us the answer by the following recurrence relation: (Segner's recurrence relation)↵
$$ C_{n+1} = \displaystyle\sum_{i=0}^{n}{C_i C_{n-i}}, n \geq 0; C_0=1 $$↵
↵
The sequence of numbers $C_0, C_1, C_2, ...$ is called **Catalan Numbers**, and for reference they are: $1, 1, 2, 5, 14, 42, ...$.↵
↵
This gives us a simple $O(n^2)$ implementation with DP, however can we do better? In fact we can, this simple recurrence formula gives out the same values:↵
↵
$$C_n = \displaystyle\frac{1}{n+1} \displaystyle{2n \choose n} = \displaystyle\frac{2n!}{n!(n+1)!}$$↵
↵
[cut]↵
↵
There are a lot of ways to prove this formula, perhaps the most common involves **generating functions** but I will attempt to prove it using another method. First off though, we will need to learn some different applications of Catalan numbers.↵
↵
Remember, any time you manage to prove that a counting problem has a solution expressed by combining two identical subproblems with total size = $n-1$, it means this problem has the same solution as all other catalan problems.↵
↵
### Balanced Parentheses count↵
↵
Find the count of balanced parentheses sequences consisting of $n$ pairs of parentheses (for example $(()(()))$ is a balanced sequence of $4$ pairs). A sequence of parentheses is balanced if each opening symbol has a corresponding closing symbol and they are properly nested, or in layman's terms: a closing bracket never appears before an opening one.↵
↵
Notice that if you consider opening brackets as a "+1" and closing brackets as a "-1", this problem is bijective to a **Dyck word** of length $2n$. A Dyck word is a word of "+1"s and "-1" such that __any__ prefix sum is never negative.↵
↵
Now, to solve our problem we can think of it using this substructure: "$($ $A$ $)$ $B$", where $A$ and $B$ are themselves valid (possibly empty) parentheses sequences. Let's denote number of pairs of parentheses in $S$ by $|S|$. Since we used one pair it follows that: $|A| + |B| = n-1$. This will make us arrive at the same recurrence relation as before, which means the answer for size $n$ is $C_n$.↵
↵
Let's however try to calculate an answer using another way: We will calculate all possible ways to arrange $n$ pairs of parentheses and then we will subtract the count of ***invalid*** sequences: Our answer is $A_n - B_n$ where $A_n$ is total number of ways, $B_n$ is the count of invalid ways.↵
↵
For starters there are $2n$ total brackets, of which $n$ are open, $n$ are close. This means $A_n = {2n \choose n}$.↵
↵
To determine $B_n$ let's define the following (notice I will use 1-based indexing here): For an invalid sequence $S$, let $k$ be the index of the earliest bracket that causes $S$ to be invalid, i.e. in $S[1..k]$: $x + 1 = y$ where $x$ is count of '$($', and $y$ is count of '$)$', in layman's terms: in the prefix up to index $k$, the count of closing brackets is exactly one more than the count of open brackets, and $k$ will be the earliest index at which this property is fulfilled.↵
↵
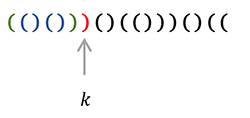↵
↵
(In this example, $n=9, k=7, X=3, Y=4$, indeed $x + 1 = y$)↵
↵
Let's define the following mapping from $S \rightarrow \hat{S}$: $\hat{S} = S[1..k] ^\frown \overline{S}[k+1..2n]$, $^\frown$ is a symbol for concatenation, $\overline{S}$ means the sequence $S$ but all open and closed brackets are swapped (inversed). Layman's speaking: Take sequence $S$, flip all brackets starting from $(k+1)$th bracket.↵
↵
The new sequence $\hat{S}$ has an interesting property, $X = n - 1, Y = n + 1$. This is easily observed intuitively, but here is a proof: by seeing that the prefix had $x$ open brackets, and $y$ closing brackets, and the original sequence had $n$ open and $n$ closing brackets. The postfix has $n-x$ and $n-y$ open and closing brackets respectively. After the transformation and adding the brackets in the prefix to the count: $X = n-y+x, Y=n-x+y$ knowing $y=x+1$: $X = n-1, Y = n+1$.↵
↵
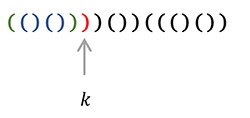↵
↵
(In this example, $X = 8, Y = 10$)↵
↵
Now, the count of such $\hat{S}$ sequences is simple: It is a sequence of length $2n$ of which $n-1$ is open, $n+1$ is close. this means $B_n = {2n \choose n-1}$. But halt right there, who's to prove that the count of $\hat{S}$ is the same as the count of bad $S$ ? To do that we need to prove that $S \rightarrow \hat{S}$ is ***bijective***, we could attempt that by proving that it is ***injective*** and ***surjective***. Oh boy...↵
↵
- **Bijective** means a one-to-one correspondence between two sets. It means that **every** item in the first set maps to **exactly one** item in the second set with no items in the second set not being mapped to. This implies that any property that applies to one of the sets, applies to the other.↵
- **Injective** means **every** item in the first set maps to **exactly one** item in the second set (no two items map to the same one), but the restriction on the second set not having unmapped items is not required.↵
- **Surjective** means that **every** item in the second set is the result of mapping of some item in the first set. i.e. every item in the second set is reachable but not necessarily by distinct ways.↵
↵
So it's clear, Bijective is basically Injective and Surjective combined. Let's attempt those proofs intuitively.↵
↵
The mapping is clearly injective because a change in $S$ carries directly to $\hat{S}$, as $k$ must be the same, and by extension, the prefix is the same between the two sequences, and the postfix is just inversed. Similarly the mapping is surjective because if you start with any $\hat{S}$, you can find index $k$ exactly as we did before, reverse the postfix $\hat{S}[k+1..2n]$ to arrive at a valid $S$. So there are no unreachable $\hat{S}$. Thus the mapping is bijective. We conclude that truly: $B_n = {2n \choose n-1}$. Since $A_n - B_n$ was just another way for us to calculate the solution of this problem, which we already know to be $n$th catalan $C_n$ it is justifiable to write:↵
↵
$C_n = A_n - B_n = \displaystyle{2n \choose n} - \displaystyle{2n \choose n-1} = \displaystyle{2n \choose n} - \displaystyle\frac{n}{n+1}\displaystyle{2n \choose n} = (1-\displaystyle\frac{n}{n+1})\displaystyle{2n \choose n} = \displaystyle\frac{1}{n+1}\displaystyle{2n \choose n}$↵
↵
Which is the thing we've been trying to prove : D↵
↵
Now to efficiently calculate $C_n$ you can manipulate the equation to find $C_n$ in terms of $C_{n-1}$ so you can use a building table to calculate it. To save you the hassle, it is: (although feel free to derive it using combination expansion, hint: expand the expression $\frac{C_n}{C_{n-1}}$)↵
↵
$C_n = \displaystyle\frac{4n - 2}{n+1} C_{n-1}, C_0 = 1$↵
↵
[CSES — Bracket Sequences I](https://cses.fi/problemset/task/2064)↵
↵
### Balanced Parentheses count with prefix↵
↵
Find the count of balanced parentheses sequences consisting of $n+k$ pairs of parentheses where the first $c$ symbols are open brackets. For instance when $n = 2, k = 2$, sequence is $((??????$. There are $9$ possible sequences that fit this pattern which are:↵
↵
- $( ( () ) () )$, $( ( () ) ) ()$, $( ( ) () ) ()$, $( ( ()() ) )$, $( ( (()) ) )$, $( ( ) ()() )$, $( ( ) (()) )$, $( ( ) ) ()()$, and $( ( ) ) (())$.↵
↵
I'll denote to the answer by $C^{(k)}_n$.↵
↵
Let's only focus on the case when $k = 2$ for now, it will be easy to generalize from there. To solve a problem with $n+k$ pairs of brackets where the sequence must start with $k$ open brackets: think of the substructure of the problem as follows: $($ $($ $A$ $)$ $B$ $)$ $C$. $A$, $B$, and $C$ are ordinary balanced bracket sequences such that their total length sum to $n$ pairs. Since count of balanced bracket sequences of size $m$ is $C_m$. It follows that the solution to our problem is:↵
↵
$$ C^{(2)}_{n} = \displaystyle\sum_{a+b+c = n}{C_a C_b C_c}, n \geq 0; C_0=1 $$↵
↵
It follows that the generalized formula is:↵
↵
$$ C^{(k)}_{n} = \displaystyle\sum_{a+b+...+\lambda = n}{C_a C_b ... C_\lambda}, n \geq 0; C_0=1 $$↵
↵
This is basically a convolution on Catalan. The number of variables is $k+1$. I will refer to this as the $k$ th convolution of Catalan.↵
↵
Here are the first few elements of $C^{(k)}_n$↵
↵
\begin{array} {|c|c|c|c|c|c|c|c|c|c|}↵
\hline↵
\textbf{k/n} & \textbf{0} & \textbf{1} & \textbf{2} & \textbf{3} & \textbf{4} & \textbf{5} & \textbf{6} & \textbf{7} & \textbf{8} \cr \hline↵
\hline ↵
\textbf{ 0 } & 1 & 1 & 2 & 5 & 14 & 42 & 132 & 429 & 1430 \cr \hline↵
\textbf{ 1 } & 1 & 2 & 5 & 14 & 42 & 132 & 429 & 1430 & 4862 \cr \hline↵
\textbf{ 2 } & 1 & 3 & 9 & 28 & 90 & 297 & 1001 & 3432 & 11934 \cr \hline↵
\textbf{ 3 } & 1 & 4 & 14 & 48 & 165 & 572 & 2002 & 7072 & 25194 \cr \hline↵
\textbf{ 4 } & 1 & 5 & 20 & 75 & 275 & 1001 & 3640 & 13260 & 48450 \cr \hline↵
\end{array}↵
Notice that when $k = 0$, the sum reduces to the trivial case $C^{(0)}_{n} = C_n$. Which confirms that Catalan numbers are themselves the $0$th convolution of catalan, this makes sense as the solution to our problems when $k=0$ is $C_n$. (Note: in books and writings I have seen, they use the term "k-fold convolution", and use a 1-based system, I see my 0-based naming better fit for our purposes here.)↵
↵
Here is the part I'm going to state without proof so excuse me :D, It can be derived (using generating functions) that:↵
↵
$$C^{(k)}_{n} = \displaystyle\frac{k+1}{n+k+1}{2n + k \displaystyle\choose n}$$↵
↵
Similar to above, a building table approach could use this for efficiently calculating it (derived using combination expansion)↵
$$C^{(k)}_{n} = \displaystyle\frac{(2n + k - 1) * (2n + k)}{n * (n + k + 1)} C^{(k)}_{n-1}$$↵
↵
(If you manage to prove this without generating functions, please tell so in the comments!)↵
↵
[CSES — Bracket Sequences II](https://cses.fi/problemset/task/2187)↵
↵
###Final points↵
↵
Thank you for reading! This is my first tutorial so I hope It is both clear and insightful! If you have any suggestions on how to improve it or caught any errors, let me know!
↵
### Binary Trees Count↵
↵
Find the count of different binary trees with $n$ nodes, we'll denote to that by $C_n$. This can be solved by observing the substructure of the problem: ↵
↵
↵
↵
From the root, the left subtree $a$ can be _any_ binary tree of size $x$, the right subtree $b$ can be _any_ binary tree of size $y$, such that $x+y=n-1$ (as we took one node as the root). With the base case at $C_0=1$ as the empty tree is a valid tree of size $0$. This directly gives us the answer by the following recurrence relation: (Segner's recurrence relation)↵
$$ C_{n+1} = \displaystyle\sum_{i=0}^{n}{C_i C_{n-i}}, n \geq 0; C_0=1 $$↵
↵
The sequence of numbers $C_0, C_1, C_2, ...$ is called **Catalan Numbers**, and for reference they are: $1, 1, 2, 5, 14, 42, ...$.↵
↵
This gives us a simple $O(n^2)$ implementation with DP, however can we do better? In fact we can, this simple recurrence formula gives out the same values:↵
↵
$$C_n = \displaystyle\frac{1}{n+1} \displaystyle{2n \choose n} = \displaystyle\frac{2n!}{n!(n+1)!}$$↵
↵
[cut]↵
↵
There are a lot of ways to prove this formula, perhaps the most common involves **generating functions** but I will attempt to prove it using another method. First off though, we will need to learn some different applications of Catalan numbers.↵
↵
Remember, any time you manage to prove that a counting problem has a solution expressed by combining two identical subproblems with total size = $n-1$, it means this problem has the same solution as all other catalan problems.↵
↵
### Balanced Parentheses count↵
↵
Find the count of balanced parentheses sequences consisting of $n$ pairs of parentheses (for example $(()(()))$ is a balanced sequence of $4$ pairs). A sequence of parentheses is balanced if each opening symbol has a corresponding closing symbol and they are properly nested, or in layman's terms: a closing bracket never appears before an opening one.↵
↵
Notice that if you consider opening brackets as a "+1" and closing brackets as a "-1", this problem is bijective to a **Dyck word** of length $2n$. A Dyck word is a word of "+1"s and "-1" such that __any__ prefix sum is never negative.↵
↵
Now, to solve our problem we can think of it using this substructure: "$($ $A$ $)$ $B$", where $A$ and $B$ are themselves valid (possibly empty) parentheses sequences. Let's denote number of pairs of parentheses in $S$ by $|S|$. Since we used one pair it follows that: $|A| + |B| = n-1$. This will make us arrive at the same recurrence relation as before, which means the answer for size $n$ is $C_n$.↵
↵
Let's however try to calculate an answer using another way: We will calculate all possible ways to arrange $n$ pairs of parentheses and then we will subtract the count of ***invalid*** sequences: Our answer is $A_n - B_n$ where $A_n$ is total number of ways, $B_n$ is the count of invalid ways.↵
↵
For starters there are $2n$ total brackets, of which $n$ are open, $n$ are close. This means $A_n = {2n \choose n}$.↵
↵
To determine $B_n$ let's define the following (notice I will use 1-based indexing here): For an invalid sequence $S$, let $k$ be the index of the earliest bracket that causes $S$ to be invalid, i.e. in $S[1..k]$: $x + 1 = y$ where $x$ is count of '$($', and $y$ is count of '$)$', in layman's terms: in the prefix up to index $k$, the count of closing brackets is exactly one more than the count of open brackets, and $k$ will be the earliest index at which this property is fulfilled.↵
↵
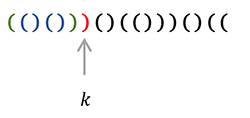↵
↵
(In this example, $n=9, k=7, X=3, Y=4$, indeed $x + 1 = y$)↵
↵
Let's define the following mapping from $S \rightarrow \hat{S}$: $\hat{S} = S[1..k] ^\frown \overline{S}[k+1..2n]$, $^\frown$ is a symbol for concatenation, $\overline{S}$ means the sequence $S$ but all open and closed brackets are swapped (inversed). Layman's speaking: Take sequence $S$, flip all brackets starting from $(k+1)$th bracket.↵
↵
The new sequence $\hat{S}$ has an interesting property, $X = n - 1, Y = n + 1$. This is easily observed intuitively, but here is a proof: by seeing that the prefix had $x$ open brackets, and $y$ closing brackets, and the original sequence had $n$ open and $n$ closing brackets. The postfix has $n-x$ and $n-y$ open and closing brackets respectively. After the transformation and adding the brackets in the prefix to the count: $X = n-y+x, Y=n-x+y$ knowing $y=x+1$: $X = n-1, Y = n+1$.↵
↵
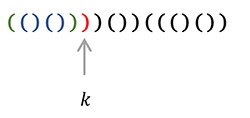↵
↵
(In this example, $X = 8, Y = 10$)↵
↵
Now, the count of such $\hat{S}$ sequences is simple: It is a sequence of length $2n$ of which $n-1$ is open, $n+1$ is close. this means $B_n = {2n \choose n-1}$. But halt right there, who's to prove that the count of $\hat{S}$ is the same as the count of bad $S$ ? To do that we need to prove that $S \rightarrow \hat{S}$ is ***bijective***, we could attempt that by proving that it is ***injective*** and ***surjective***. Oh boy...↵
↵
- **Bijective** means a one-to-one correspondence between two sets. It means that **every** item in the first set maps to **exactly one** item in the second set with no items in the second set not being mapped to. This implies that any property that applies to one of the sets, applies to the other.↵
- **Injective** means **every** item in the first set maps to **exactly one** item in the second set (no two items map to the same one), but the restriction on the second set not having unmapped items is not required.↵
- **Surjective** means that **every** item in the second set is the result of mapping of some item in the first set. i.e. every item in the second set is reachable but not necessarily by distinct ways.↵
↵
So it's clear, Bijective is basically Injective and Surjective combined. Let's attempt those proofs intuitively.↵
↵
The mapping is clearly injective because a change in $S$ carries directly to $\hat{S}$, as $k$ must be the same, and by extension, the prefix is the same between the two sequences, and the postfix is just inversed. Similarly the mapping is surjective because if you start with any $\hat{S}$, you can find index $k$ exactly as we did before, reverse the postfix $\hat{S}[k+1..2n]$ to arrive at a valid $S$. So there are no unreachable $\hat{S}$. Thus the mapping is bijective. We conclude that truly: $B_n = {2n \choose n-1}$. Since $A_n - B_n$ was just another way for us to calculate the solution of this problem, which we already know to be $n$th catalan $C_n$ it is justifiable to write:↵
↵
$C_n = A_n - B_n = \displaystyle{2n \choose n} - \displaystyle{2n \choose n-1} = \displaystyle{2n \choose n} - \displaystyle\frac{n}{n+1}\displaystyle{2n \choose n} = (1-\displaystyle\frac{n}{n+1})\displaystyle{2n \choose n} = \displaystyle\frac{1}{n+1}\displaystyle{2n \choose n}$↵
↵
Which is the thing we've been trying to prove : D↵
↵
Now to efficiently calculate $C_n$ you can manipulate the equation to find $C_n$ in terms of $C_{n-1}$ so you can use a building table to calculate it. To save you the hassle, it is: (although feel free to derive it using combination expansion, hint: expand the expression $\frac{C_n}{C_{n-1}}$)↵
↵
$C_n = \displaystyle\frac{4n - 2}{n+1} C_{n-1}, C_0 = 1$↵
↵
[CSES — Bracket Sequences I](https://cses.fi/problemset/task/2064)↵
↵
### Balanced Parentheses count with prefix↵
↵
Find the count of balanced parentheses sequences consisting of $n+k$ pairs of parentheses where the first $c$ symbols are open brackets. For instance when $n = 2, k = 2$, sequence is $((??????$. There are $9$ possible sequences that fit this pattern which are:↵
↵
- $( ( () ) () )$, $( ( () ) ) ()$, $( ( ) () ) ()$, $( ( ()() ) )$, $( ( (()) ) )$, $( ( ) ()() )$, $( ( ) (()) )$, $( ( ) ) ()()$, and $( ( ) ) (())$.↵
↵
I'll denote to the answer by $C^{(k)}_n$.↵
↵
Let's only focus on the case when $k = 2$ for now, it will be easy to generalize from there. To solve a problem with $n+k$ pairs of brackets where the sequence must start with $k$ open brackets: think of the substructure of the problem as follows: $($ $($ $A$ $)$ $B$ $)$ $C$. $A$, $B$, and $C$ are ordinary balanced bracket sequences such that their total length sum to $n$ pairs. Since count of balanced bracket sequences of size $m$ is $C_m$. It follows that the solution to our problem is:↵
↵
$$ C^{(2)}_{n} = \displaystyle\sum_{a+b+c = n}{C_a C_b C_c}, n \geq 0; C_0=1 $$↵
↵
It follows that the generalized formula is:↵
↵
$$ C^{(k)}_{n} = \displaystyle\sum_{a+b+...+\lambda = n}{C_a C_b ... C_\lambda}, n \geq 0; C_0=1 $$↵
↵
This is basically a convolution on Catalan. The number of variables is $k+1$. I will refer to this as the $k$ th convolution of Catalan.↵
↵
Here are the first few elements of $C^{(k)}_n$↵
↵
\begin{array} {|c|c|c|c|c|c|c|c|c|c|}↵
\hline↵
\textbf{k/n} & \textbf{0} & \textbf{1} & \textbf{2} & \textbf{3} & \textbf{4} & \textbf{5} & \textbf{6} & \textbf{7} & \textbf{8} \cr \hline↵
\hline ↵
\textbf{ 0 } & 1 & 1 & 2 & 5 & 14 & 42 & 132 & 429 & 1430 \cr \hline↵
\textbf{ 1 } & 1 & 2 & 5 & 14 & 42 & 132 & 429 & 1430 & 4862 \cr \hline↵
\textbf{ 2 } & 1 & 3 & 9 & 28 & 90 & 297 & 1001 & 3432 & 11934 \cr \hline↵
\textbf{ 3 } & 1 & 4 & 14 & 48 & 165 & 572 & 2002 & 7072 & 25194 \cr \hline↵
\textbf{ 4 } & 1 & 5 & 20 & 75 & 275 & 1001 & 3640 & 13260 & 48450 \cr \hline↵
\end{array}↵
Notice that when $k = 0$, the sum reduces to the trivial case $C^{(0)}_{n} = C_n$. Which confirms that Catalan numbers are themselves the $0$th convolution of catalan, this makes sense as the solution to our problems when $k=0$ is $C_n$. (Note: in books and writings I have seen, they use the term "k-fold convolution", and use a 1-based system, I see my 0-based naming better fit for our purposes here.)↵
↵
Here is the part I'm going to state without proof so excuse me :D, It can be derived (using generating functions) that:↵
↵
$$C^{(k)}_{n} = \displaystyle\frac{k+1}{n+k+1}{2n + k \displaystyle\choose n}$$↵
↵
Similar to above, a building table approach could use this for efficiently calculating it (derived using combination expansion)↵
$$C^{(k)}_{n} = \displaystyle\frac{(2n + k - 1) * (2n + k)}{n * (n + k + 1)} C^{(k)}_{n-1}$$↵
↵
(If you manage to prove this without generating functions, please tell so in the comments!)↵
↵
[CSES — Bracket Sequences II](https://cses.fi/problemset/task/2187)↵
↵
###Final points↵
↵
Thank you for reading! This is my first tutorial so I hope It is both clear and insightful! If you have any suggestions on how to improve it or caught any errors, let me know!





