See https://twitter.com/cHHillee/status/1732868066558792189 for the original tweet. Contents mimicked below.

TL;DR: I found AlphaCode2 accounts, and through stalking their submission history, I manually performed the AlphaCode2 Codeforces evals, and found the model to perform at about a ~1650 rating.

I am somewhat concerned about data leakage, see https://twitter.com/cHHillee/status/1732636161204760863. This is an AlphaCode2 contributor's response https://twitter.com/RemiLeblond/status/1732677521290789235 However, for the purposes of this analysis I'll take the results at face value.

Methodology

Disclaimer: I'm trying to reverse-engineer info from their public submissions, so apologies in advance for any errors.

There is a fixed set of 12 contests that they submit to. When they kick off a "run" they submit to these contests from several accounts at a time.

As far as I can tell they didn't do extensive evals on other contests. They performed most of their evaluation between the middle of october and november, and they repeatedly eval on the same set of contests.

Identifying their accounts is pretty easy. They all have the form <noun, usually animal>.

To find a full "eval" run, I found a particular time that they started submitting. For example, October 25th around 10pm. Generally, there are at least 10 submissions for every problem across all accounts. I then went down all submissions done to the contest, and noted down which submissions were made by AC2 accounts around the time.

For each contest, I note down whether any of the accounts solved it and how many incorrect submissions they had before the first accepted submission.

For example, for 1810, they solved A,B,C, and G. B took 6 incorrect submissions before acceptance.

As you folks know, Codeforces also has a penalty (either less points or a completely separate penalty score) depending on the submission time + # of incorrect submissions. I compute the penalty using the approach mentioned in the paper, where AC2 makes submissions throughout the contest. I also compute a penalty assuming instant submission, since in some sense, AC2 having a "speed edge" is fair when comparing it against humans.

Then, for the given score/results for the model, I manually expect the leaderboard to find the "rating" that the model performs at. For example, for contest 1837 3 problems solved + 118 penalty results in a 1104 rating.

Overall, after repeating this procedure for 11 (I skipped one contest) of the contests, I arrive at a final rating of 1630 with 43% of the problems solved! This is a 400 rating improvement over the original AlphaCode2.

This is already better than many humans, which is pretty impressive.

One concern I had about this eval is whether this "run" actually represented their performance, or whether it was using a worse model or something like that for this run. So, for every problem that wasn't solved, I checked whether there were any AlphaCode2 submissions that solved the problem. There were only 2 problems that AlphaCode2 ever solved that this particular run didn't. And those runs failed on other problems.

Concerns

Now, some hesitance. The first is the reliance on pretests. Codeforces provides sample inputs for each problem, and especially on easy problems, these sample inputs are often quite "strong" and informative.

AlphaCode2 submits a lot of wrong answers.

And these submissions already pass the pretest! I would expect that on problems without informative pretests (quite common among harder ratings or say, constructive problems) AC2's performance suffers drastically.

For example, no AC2 run solved this 1200 rated problem (https://mirror.codeforces.com/contest/1834/problem/C) and not for a lack of trying. I'm guessing because the pretests weren't informative enough for the filtering to work well.

In addition, it doesn't solve many hard problems. Other than the problem identified in the press release, the hardest problems it solves are a 2200, 2100, 1800 and an 1700. It solves nothing else above 1600. This is partially why solving the 3200 rated stands out so much!

Also, AC2 generally benefits quite a bit from solving problems "quickly". Compared to other contestants around its level, it's generally solving easy problems very fast.

e.g. On CF round 880, it obtains 2196 rating. But everybody down to 1640 solved the same problems.

I also find the contest selection a bit unusual. One note is that when the paper says "Div 2" and "Div 1 + 2" contests, they mean 11 Div 2 contests and a single Div 1+2 contest (which is also where AC2 solved its hardest problem).

Another question is why they chose the contests they evaled on?

My particular qualms 1. why choose a relatively old set of contests? AFAICT, the evals were performed in Oct/Nov, but the latest contest is from June. 2. Why not a contiguous set of contests? For example, contest 1844 was skipped despite doing contest 1841 and 1845.

In addition, one of the contests (https://mirror.codeforces.com/contest/1814) was declared non-rated halfway through the contest! Undoubtedly, many contestants stopped participating at this point, leading to a skewed distribution of performance.

Conclusion

Overall, great work from the AC2 team! Solid progress over AC1, although perhaps not enough that I think competitive programming will be solved imminently :)

I'd love to see more transparency (maybe a live evaluation?), but I understand their hands are tied.

And here's my datasheet where I tracked my manual eval of AlphaCode2

This blog post brought to you by pajenegod, Narut, and the rest of #constant-factor on the AC discord server. If you're interested in discussions like this, feel free to join!

For the longest time, CF has constrained us to the tyranny of 32 bit C++. Not only has that slowed down our long long operations, it has also constrained us to a measly 32 bit constant factor reduction with bitsets!

Let's take 2 pieces of equivalent code.

For Loop:

int a[MAXN], b[MAXN]
for (int it = 0; it < iters; it++) 
    for (int i = 0; i < MAXN; i++) 
        if (a[i] & b[i]) cnt++;

Bitset:

bitset<MAXN> a, b;
int cnt = 0;
for (int it = 0; it < iters; it++) 
    cnt += (a | b).count();

On Custom Invocation C++17 (32 bit) for MAXN=1e4 and iters=1e5, this boring for loop code runs in 3594 ms, while the equivalent bitset version runs in 104ms. 3594/104 is approximately 32. Ok, disappointing but makes sense.

However, Mike, in his generosity, has recently decided to free us from our chains, and give us 64 bit C++! Just imagine, 64x constant factor improvements vs 32x! However, what happens if we try our previous benchmark?

For Loop (C++17 64 bit): 3736 ms
Bitset (C++17 64 bit): 107ms

What's going on?

Huh? What gives? Have we been lied to? Where are our improvements? I'm not alone in noting this, see tribute_to_Ukraine_2022's comment here

So, what's the problem? The answer, as it so often is, is Windows. On Windows, long is always defined to be 32 bits, regardless of what the underlying OS is using.

And as it turns out, GCC bitset uses long as it's data type! Which means that even though our compiled code can use 64 bit instructions, the implementation of STL bitset is artificially constraining us! >:(

Misuse of Macros

So the STL is implemented in a way that forces us into 32 bit bitset. Are we screwed? No! As it turns out, before PL people realized how good of an idea namespaces were, they gave us the C++ macro and #include systems! Thus, even though you're importing code that you have no control over, you can actually modify its internals through shameless abuse of macros.

For example, say your colleague's heard of something called "encapsulation" or "abstraction", and made the internals of his data structure private so you can't modify them. Obviously, you're smarter than they are, and now you need to modify the internals of his data structure. You could ask them — or you could #define private public!

We can use a similar idea here, where we want to replace long with long long. In principle, #define unsigned unsigned long would work. Unfortunately, the GCC programmers never thought of such a brilliant usage of their library, and this breaks their internal code. I won't go through the entire process of what we needed to do, so let me present: 64 bit bitsets on Codeforces!

64 bit bitsets!

#include <string>
#include <bits/functexcept.h>
#include <iosfwd>
#include <bits/cxxabi_forced.h>
#include <bits/functional_hash.h>

#pragma push_macro("__SIZEOF_LONG__")
#pragma push_macro("__cplusplus")
#define __SIZEOF_LONG__ __SIZEOF_LONG_LONG__
#define unsigned unsigned long
#define __cplusplus 201102L

#define __builtin_popcountl __builtin_popcountll
#define __builtin_ctzl __builtin_ctzll

#include <bitset>

#pragma pop_macro("__cplusplus")
#pragma pop_macro("__SIZEOF_LONG__")
#undef unsigned
#undef __builtin_popcountl
#undef __builtin_ctzl

#include <bits/stdc++.h>

using namespace std;

signed main() {
    bitset<100> A;
    A[62] = 1;
    cout << A._Find_first()<<endl;
}

If we rerun our benchmarks, we see

For Loop (C++17 64 bit): 3736 ms
Actually 64 bit Bitset (C++17 64 bit): 69ms

Ah... 3736/69 ~= 64. There we go :)

Running the benchmarks with MAXN=1e5 and iters=1e5 makes it more obvious.

Bitset (C++17 64 bit): 908 ms
Actually 64 bit Bitset (C++17 64 bit): 571ms

Real Problems

Let's take a real problem Count the Rectangles, code taken from okwedook here.

Adding our "template" speeds up his solution from 373ms to 249ms!

Caveats

Hm... None that I can see :^)

Note: This code is provided with no warranty. If you get WA, TLE, or your code crashes because of this template, don't blame me.

In Codeforces Round #637 (Div 1), pajenegod became the first Python user (to my knowledge) to become Grandmaster, with a rating of 2464!

Considering how much Python is derided by most of the people in the CP community, some people thought this was impossible. pajenegod has truly mastered writing cancer code in Python. Feel free to PM him for all of your Python needs :^)

* Sadly, this round retroactively became unrated. So I made this thread for posterity.

As coronavirus concerns ramp up, I'm starting to become worried about what ICPC's plans for World Finals are. Many schools (Cornell, Harvard, MIT, Princeton, etc.) are all forcing students to leave campus soon.

Giving these conditions, I'm curious what plans for World Finals are going to be. Has anybody heard about any contingency plans — for example, multiple sites?

Alternatively, does anybody know if there's any precedent for what happens in this kind of event?

http://web.stanford.edu/class/cs166/handouts/100%20Suggested%20Final%20Project%20Topics.pdf

Some of the ones listed are somewhat par for the course for advanced CP'ers (Range Queries, RMQ for LCA, Suffix Automaton, Ukkonen's Algorithm), but most of them are ones I've never heard about.

In addition to describing the data structure, they also give a "Why they're worth studying". Pretty cool! I wonder if there's any others that are relevant for CP.

In various places(12), people have talked about "Dinic's With Scaling" having $$$O(VElog(U))$$$ complexity, where U is the max edge capacity. However, in just as many places, people have cast doubt about this complexity or worried that this algorithm ends up being slower in practice(12).

I had the same doubts. In fact, a couple months ago I benchmarked Dinic's with scaling on some hard test cases and thought that Dinic's with/without scaling performed similarly.

As it turns out, I benchmarked it again yesterday and found that Dinic's with scaling definitely has significantly better asymptotic complexity (by a factor of V).

Synthetic Benchmarking

I used the hard test case generator at 2 posted by ko_osaga here. The one posted at 1 creates a graph with only V edges and moreover, doesn't work for me... Notably, given a V, it generates a graph with V nodes and $$$O(V^2)$$$ edges.

The code I used was my own Dinic's implementation (originally from emaxx) found here. Notably, the SCALING variable toggles between Dinic's with scaling and without. It's a small change, as you can see.

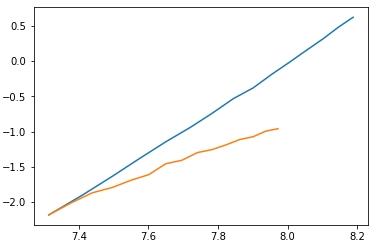I ran the two code across a variety of input sizes, averaging across 10 runs, then taking the log of input size and times, plotting them in a where blue is the runtime of Dinic's without scaling and orange is the runtime of Dinic's with scaling. Since the important thing to look at is the slope of the line, I normalized the lines to start at the same point.

Fitting a linear regression to the points, we see that the slope of Dinic's without scaling is 3.204, while the slope of Dinic's with scaling is 1.93, which correspond to complexities of $$$O(V^3)$$$ and $$$O(V^2)$$$ respectively.

In terms of actual runtime, here are some numbers on specific sizes.

Benchmarking on Problems

There are 3 flow problems, I benchmarked on — SPOJ FASTFLOW, (VNSPOJ FASTFLOW)[https://vn.spoj.com/problems/FFLOW/), and a Chinese LOJ Flow Problem (it's intended to solve this problem with Highest Label Preflow Push, which has $$$O(V^2\sqrt{E})$$$ complexity).

Also, to vouch for my implementation, here's some benchmarks with other implementations :^) Mine (to enable scaling change the SCALING boolean), Emaxxs dinic,LOJ fastest (HLPP, the fastest submission on the Chinese flow problem). As I was doing these benchmarks I realized the LOJ submission is actually faster than mine on all of my benchmarks :'(. It is substantially longer than my implementation though :^)

SPOJ (V<=5000, E<=3e4)
Mine: 0.04
Emaxx Dinic: 0.11
Mine w/ scaling: 0.27
LOJ fastest: 0.00

VNSPOJ (V<=5000, E<=3e4, harder test cases):
Mine: TLE
Emaxx dinic: TLE
Mine w/ scaling: 0.00
LOJ fastest: 0.00

LOJ (V<=1200, E<=120000):
Mine: 56 points
Mine w/ scaling: 88 points
Emaxx dinic: 44 points
LOJ fastest: AC, 1176 ms total, #1 on leaderboard

Synthetic Test(N=2000, E=4e6):
Mine: 66.56
Emaxx dinic: 247.40
Mine w/ scaling: 0.14
LOJ fastest: 0.10

Number of non-whitespace characters:
Mine: 1164
Emaxx dinic: 1326
LOJ fastest: 2228

Conclusions:

First off, HLPP seems to be superior to Dinic's in terms of runtime, so perhaps the real lesson is that people should be using HLPP. Also, I hope to provide a solid well-tested implementation of Dinic's with scaling that people can use. Other than that, however, I hope it's clear that Dinic's with scaling really does have a significant improvement in runtime (approximately a factor of V), and that translates to significantly better performance on real problems.

PS: If anyone has a flow implementation they think is better than mine, I'd like to see it :^)

One of my favorite implementations of segment trees has always been "Easy and Efficient Segment Trees, by Al.Cash. I used to dread segtree problems, but after reading that blog post and adapting a super simple implementation I've gotten a lot better with them. However, there are some types of segtree that you can't implement in that fashion, namely dynamic segtrees and persistent segtrees. See here for criticism. With the advent of policy hash tables, however, one can now implement dynamic segtrees in Al.Cash's style with somewhat comparable performance to a custom dynamic segtree.

Standard segtree

This is how a standard segtree looks like. You can set a single element, and query for ranges. It's nice and simple, and I think it's a great implementation.

int N;
int seg[2 * MAXN];

void modify(int p, int val) {
    for (seg[p += N] = val; p > 0; p >>= 1)
        seg[p >> 1] = seg[p] + seg[p ^ 1];
}

int query(int l, int r) {
    int res = 0;
    for (l += N, r += N; l < r; l >>= 1, r >>= 1) {
        if (l & 1)
            res += seg[l++];
        if (r & 1)
            res += seg[--r];
    }
    return res;
}

Dynamic Segtree

However, say your underlying array had 1e9 possible locations, but it only contained 1e5 elements. For example, take a look at this post. Obviously, you can't store all 2e9 elements in your segtree, so what should you do? Here's one solution, replace the array with a hash table. However, as adamant mentions, unordered_map has too much overhead. We'll be benchmarking against the dynamic segtree provided here. I'll also be using a custom hash function. So to be clear, the implementation now looks like:

int N;
unordered_map<int, int, chash> seg;

void modify(int p, int val) {
    for (seg[p += N] = val; p > 0; p >>= 1)
        seg[p >> 1] = seg[p] + seg[p ^ 1];
}

int query(int l, int r) {
    int res = 0;
    for (l += N, r += N; l < r; l >>= 1, r >>= 1) {
        if (l & 1)
            res += seg[l++];
        if (r & 1)
            res += seg[--r];
    }
    return res;
}

And benchmarking it with 1e5 random insertions and 1e5 random queries.

pointer: 0.171485
unordered_map: 2.0646

Wow. The unordered_map is nearly 12x slower. That's not really feasible for a lot of contests. What if we replace it with a policy hash table, though?

int N;
unordered_map<int, int, chash> seg;

void modify(int p, int val) {
    for (seg[p += N] = val; p > 0; p >>= 1)
        seg[p >> 1] = seg[p] + seg[p ^ 1];
}

int query(int l, int r) {
    int res = 0;
    for (l += N, r += N; l < r; l >>= 1, r >>= 1) {
        if (l & 1)
            res += seg[l++];
        if (r & 1)
            res += seg[--r];
    }
    return res;
}

pointer: 0.202186
policy hash table: 0.384312

Only a 2x decrease in speed. That's already very feasible. However, one might notice that since maps in C++ create elements if you try to access a key that doesn't exist, we're creating a lot of useless elements. Thus, we can simply wrap a check to make sure the element is in the array before we try to access it

EDIT: Updated with dalex's optimization.

gp_hash_table<ll, ll, chash> seg;

ll get(ll x) { return (seg.find(x) == seg.end()) ? 0 : seg[x]; }
void modify(ll p, ll val) {
    for (seg[p += N] = val; p > 0; p >>= 1) {
        seg[p >> 1] = get(p) + get(p ^ 1);
    }
}

ll query(ll l, ll r) {
    ll res = 0;
    for (l += N, r += N; l < r; l >>= 1, r >>= 1) {
        if (l & 1)
            res += get(l++);
        if (r & 1)
            res += get(--r);
    }
    return res;
}

Results (averaged over twenty runs):

2e5 insertions and 2e5 queries

pointer: 0.44085
policy hash table: 0.57878

1e5 insertions and 1e5 queries

pointer: 0.19855
policy hash table: 0.29467

1e4 insertions and 1e4 queries

pointer: 0.014
policy hash table: 0.027

So while we're nearly twice as slow with 1e4 elements and 1e4 queries, we're actually only 30% slower with 2e5 insertions and 2e5 queries.

One more thing. While I'm giving numbers like "30% slower", that's a little bit misleading. If we break down the numbers between insertion/querying, we see this:

2e5 insertions and 2e5 queries Queries:

pointer: 0.41625
policy hash table: 0.15627

Insertions:

pointer: 0.1367
policy hash table: 0.42619

1e4 insertions and 1e4 queries Queries:

pointer : 0.094
policy hash table: 0.007

Insertions:

pointer : 0.0045
policy hash table: 0.0191

So as we see from this more granular breakdown, the Policy Hash Table implementation is actually ~3x faster at querying than the custom implementation, while the custom implementation is roughly ~3x faster at inserting elements.

TL;DR: Using policy hash tables is an extremely easy and fairly efficient method of implementing dynamic segtrees.

TL;DR

The Policy Hash Table has 3-6x faster insertion/deletion and 4-10x increase for writes/reads. As far as I can tell, there are no downsides. The policy hash table (specifically the open-addressing version), beats out unordered_map in all my benchmarks.

PS: Make sure you read the section a better hash function and use it — I'd recommend this one: https://github.com/kth-competitive-programming/kactl/blob/master/content/data-structures/HashMap.h

Background

I've often been irritated by how slow unordered_map is in C++. Too often, I have something that runs fast enough in terms of complexity, but the constant factor from unordered_map slows down the solution too much. Yesterday though, after using the useful order statistics tree from https://mirror.codeforces.com/blog/entry/11080, I was curious if there were any other useful data structures hiding in the Policy STL. And lo and behold, I found a hash table.

Benchmarks

Well, enough backstory, let's look at some numbers. All benchmarks below are compiled with C++14 -O2.

unordered_maplinear insertion:                                  0.689846
cc_hash_tablelinear insertion:                                  0.408233
gp_hash_tablelinear insertion:                                  0.256131

unordered_maplinear read/write:                                 1.69783
cc_hash_tablelinear read/write:                                 0.202474
gp_hash_tablelinear read/write:                                 0.26842

unordered_maprandom insertion:                                  2.90184
cc_hash_tablerandom insertion:                                  3.15129
gp_hash_tablerandom insertion:                                  0.56553

unordered_maprandom read/write:                                 2.02336
cc_hash_tablerandom read/write:                                 0.333415
gp_hash_tablerandom read/write:                                 0.403486

While for linear insertions, the policy hash table gives modest improvements, the policy hash table blows the unordered_map out of the water when it comes to reads/writes. These are order of magnitude improvements that make hash tables usable when they previously weren't. "Official" benchmarks done by the DS authors can also be found here

Example

Benchmarks of course, don't always reflect the real world. So here's an example of it allowing a solution to be accepted that TLE's with unordered_map.

Example problem (5000 ms time limit)
Solution with unordered_map: (TLE on test case 8)
Solution with policy hash table directly substituted in: (TLE on test case 26)
Solution with unordered_map, rewritten to not use clears: (TLE on test case 26)
Solution with policy hash table and rewritten to not use clears: (AC with max time of 3180 ms)

Usage

To use this data structure:

#include <ext/pb_ds/assoc_container.hpp>
using namespace __gnu_pbds;
gp_hash_table<int, int> table;

From there, the API seems almost exactly the same.

Defeating Anti-Hash tests

One weakness of hash tables is that mean people can find hash collisions offline and blow up the complexity of your hashmap. In my opinion, the easiest way of solving this is below. There's no need to define your own custom hash function.

const int RANDOM = chrono::high_resolution_clock::now().time_since_epoch().count();
struct chash {
    int operator()(int x) const { return x ^ RANDOM; }
};
gp_hash_table<key, int, chash> table;

Why is it so much faster?

See my comment here

A better hash function

There is one issue with using policy hash tables as is. The default hash function for numerics in C++ is just the identity. This is especially problematic for using hash tables for something like a fenwick tree, especially since the default bucket structure for policy_hash_tables is based of powers of 2 and not primes. If you're using policy hash tables for fenwick trees, you have 2 options. 1. Choose to use prime table sizes, as done here. 2. Choose a better hash function for integers, as done here.

Thanks to adamant for his post that revealed to me the existence of policy data structures, and thanks to ed1d1a8d for the discussion.

PS: In other posts for unordered_map, I've seen people claim that reserve and max_load_factor could increase performance drastically. They didn't seem to do much for me. However, if you want to do something similar for these hash tables, check out the example here

Code for the benchmarks can be found here

EDIT: I realized that gp_hash_table is the way to go, not cc_hash_table. gp_hash_table sacrifices ~10% reading/writing speed to gain 3-6x in insertion/deletion/clearing. I updated the post to reflect the new numbers.

It seems that in C++11, even with the standard ios::sync_with_stdio(0), cin.tie(0); hacks, has significantly slower I/O with cin/cout than C++14.

View these submissions:
- cin/cout && C++11: 2963ms here
- cin/cout && C++14: 1934ms here

With scanf/printf, this issue isn't there:
- scanf/printf && C++11: 2027ms here
- scanf/printf && C++14: 1887ms here

I was unaware of this. Does anybody have any explanations? Am I missing something specific about my submissions?

Thanks ed1d1a8d for the discussion.

So I've been trying to solve this problem recently.

http://main.edu.pl/en/archive/oi/20/gob

My current solution is this:

For each contiguous dark segment, extend a line that passes through the dark segment's endpoints. The position to place the lantern must lie on all of these lines.

Second, for the walls that are completely illuminated, we can create half planes from that, with which we can find points that can reach all walls. This process will give us a polygon. The position obtained from using the dark segments must lie inside this polygon.

However, I am not satisfied that this is the right solution. Compared to the other problems in this contest, it seems far more difficult to implement. In addition, there seems to be many corner cases involved in this problem as well, leading to an inelegant solution. I fear I have missed an obvious solution, and decided to post here to make sure.

Thanks