В данной задаче нужно было для каждого яблока определить, кому оно нравится, и отдать его этому хомяку. Так как гарантировалось, что ответ существует, то каждое яблоко нравилось либо Александру, либо Артуру.
В данной задаче нужно было проверить, что заданная строка является палиндромом, и что она состоит только из симметричных символов. Симметричные символы — AHIMOTUVWXY.
Прежде всего, добавим в ответ всех людей, которые ни разу не упоминались в сообщениях. Далее рассмотрим два случая.
1) Есть участник с номером i такой, что первое сообщение с его участием - i.
Рассмотрим всех таких участников. Среди них выберем того, первое упоминание о котором встречается позже остальных. Тогда лишь он может быть лидером, так как другие ушли раньше, а те участники, о которых первое сообщение начинается с « + », не могут быть лидерами, так как когда они пришли i уже был. Но нужно проверить, может ли он на самом деле быть лидером (так как например, может он ушел, а потом сразу пришел кто-то другой). Для этого добавим в начало сообщений всех участников, для которых первое сообщение начинается с « - » в порядке их появления. То есть сначала добавим того, кто ушел раньше остальных (он упоминается первым), затем того, кто ушел вторым, и так далее. В конце добавим нашего кандидата на лидера (то есть в итоге он будет первым в списке сообщений). После добавления проверим описанным ниже алгоритмом по списку сообщений и кандидату, может ли он быть лидером.
2) Для всех участников первая запись о них начинается с « + ».
Тогда, очевидно, кандидатом на лидера может быть только участник, который появился в митинге самым первым. Проверим алгоритмом его.
Алгоритм проверки, может ли заданный кандидат быть лидером, очень прост. Поддерживаем set участников, которые в данный момент есть в митинге. Идем по списку сообщений и добавляем или удаляем соответствующих участников. Перед и после каждой операцией проверяем, что если список участников не пуст, то наш кандидат должен в нем присутствовать.
Хитрыми тестами в этой задаче оказались тесты 33 и 34, на которых упали решения многих участников. Тест 33 выглядит так.
4 4
+ 2
- 1
- 3
- 2
Здесь лидером может быть только 4-ый участник (в предположении, что он всегда находится на митинге). Второй не может быть лидером, так как изначально он не участвовал в митинге, а первый и третий участвовали. Но они тоже не могут быть лидерами, так как вышли из митинга в то время, когда там находился второй участник.
Тест 34 следующий.
3 3
- 2
+ 1
+ 2
В данном тесте лидером может быть только 3-ий участник. Второй изначально находится на митинге, потом уходит, но далее приходит первый, поэтому второй не может быть лидером. Первый не может быть лидером, потому что он изначально не находится на митинге, а второй участник находится.
Давайте построим неориентированный граф, вершины которого — это люди, а ребро между двумя людьми a, b есть, если существует высказывание человека (виноват a или b). Как теперь переформулируется задача в терминах этого графа? Нужно посчитать количество таких пар вершин, что им инцидентно как минимум p ребер.
Сделаем следующее. Сохраним граф в виде списков смежности, а также создадим массив степеней всех вершин графа и отсортируем его. Будем перебирать одну вершину и считать, сколько существует вершин в пару ей, чтобы получилась нужная пара вершин. Первое, что приходит в голову — это для каждой вершины v добавить к ответу количество вершин u таких, что d[u] + d[v] ≥ p (количество таких вершин можно просто посчитать бинарным поиском, например). К сожалению, это неправильно, поскольку в сумме d[u] + d[v] ребра между v и u учитываются два раза.
Но, давайте посчитаем ответ неправильно, а потом учтем все то, что мы неправильно посчитали. А именно, для каждой вершины пройдемся по списку ее соседей и для каждого уникального соседа вычтем его из ответ, если он добавился туда (если d[v] + d[u] ≥ p). Теперь осталось учесть в ответе все вершины, которые смежны в графе. Это делается простым проходом по ребрам.
Обратите внимание, что в этой задаче в графе могут получиться мультиребра, их нужно аккуратно обрабатывать.
Решение состоит из двух этапов.
1) Определим возможную исходную перестановку.
Будем идти по заданным запросам. Пусть текущий запрос утверждает, что число a стоит на позиции b. Если a уже раньше встречалось, то пропустим такой запрос. Иначе определим, на какой позиции находится a в искомой перестановке.
Пусть мы уже знаем, что в искомой перестановке число a1 стоит на позиции b1, a2 на позиции b2, ..., ak на позиции bk (b1 < b2 < ... < bk). Так как после объявления позиции числа оно перемещается в самое начало перестановки, то значит до того как мы объявили о позиции a все ai (1 ≤ i ≤ k) уже находятся перед a. Но при этом некоторые из этих ai уже находились раньше a в искомой перестановке, а остальные находились позже, но переместились вперед. Найдем их количество. Для этого нужно найти такую свободную позицию p в исходной перестановке, что p + x = b, где x — количество bi таких, что bi > x.
Это можно найти с помощью дерева отрезков следующим образом. Будем хранить в вершине дерева отрезков количество уже занятых позиций искомой перестановки на соответствующем подотрезке. Предположим, мы хотим найти p в некотором поддереве. Посмотрим на минимальную позицию в правом поддереве prg и на количество занятых там позиций xrg. Тогда если prg + xrg ≤ b, то нужно продолжать искать в правом поддереве. Если же prg + xrg > b, то нужно продолжать искать в левом поддереве, уменьшив при этом b на величину xrg. Когда мы нашли p, проверим выполнение условия p + x = b. Если оно не выполняется, то ответ - 1.
2) Проверим, что последовательность операций корректная.
Пусть мы рассматриваем i-ый запрос, утверждающий, что число a стоит на позиции b. Нужно проверить, что он верен. Если a раньше не встречалось в запросах, то запрос верен, так как мы проверили b еще на первом этапе. Если оно раньше встречалось, найдем такое максимальное j < i, что j-ый запрос также объявляет, в какой позиции находится a. После j-го запроса a перемещается в начало перестановки, а далее другие числа могут передвигать его вправо. Найдем количество различных таких чисел на отрезке запросов [j + 1, i - 1], их должно быть ровно b - 1.
Скажем, что в данной задаче у нас есть луч, на котором есть бесконечное число шариков, находящихся на расстояниях, кратных d от начала луча. Заметим, что хотя бы один шарик, который будет посчитан в ответе должен упираться в границу какого-нибудь круга. Также заметим, что если мы рассмотрим любой круг, то количество углов a на которые нужно повернуть наш луч так, чтобы какой-нибудь из шариков лежал на границе этого круга не превосходит 4 * r / d. Назовем такие углы критическими.
Выпишем все возможные критические углы от всех окружностей в массив B и отсортируем его. Далее для каждой окружности выпишем ее критические углы и отсортируем. Тогда между двумя соседними критическими углами количество шаров, попадающих в круг будет постоянно. Посчитаем k это количество, найдем данные углы в B. Тогда повернув луч на любой угол, находящийся между ними, к ответу будет прибавляться k.
Заведем массив C такой, что Ci — ответ, если мы повернули луч на угол Bi. Тогда после того как мы нашли k и позиции углов в B, нужно сделать прибавление на отрезке в массиве C. После того как мы обработаем все критические углы всех кругов нужно найти максимум в массиве C.









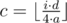 — сколько полных кругов пробежит Валера по стадиону. Тогда на своем последнем кругу Валера уже пробежал
— сколько полных кругов пробежит Валера по стадиону. Тогда на своем последнем кругу Валера уже пробежал 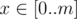 в
в 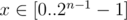 . Среди таких
. Среди таких 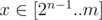 , среди них найти максимальное
, среди них найти максимальное 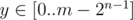 и прибавить к нему
и прибавить к нему 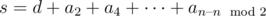 . При этом минимальное число, которое мы сможем набрать
. При этом минимальное число, которое мы сможем набрать 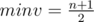 , а максимальное –--
, а максимальное –-- 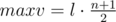 .
. 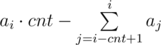 . Если эта величина не превосходит
. Если эта величина не превосходит 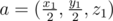 и вектор нормали к плоскости, содержащей эту грань, который направлен в сторону от внутренности параллелепипеда, то есть
и вектор нормали к плоскости, содержащей эту грань, который направлен в сторону от внутренности параллелепипеда, то есть 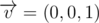 . Рассмотрим также вектор
. Рассмотрим также вектор 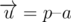 . Если неориентированный угол между этими векторами меньше
. Если неориентированный угол между этими векторами меньше 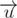 и
и 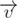 , и если оно строго больше нуля, то угол будет подходящим.
, и если оно строго больше нуля, то угол будет подходящим.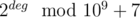 , так как каждый цикл (1-вершина) увеличивает количество возможных путей вдвое (потому что в цикле из одной вершины в другую можно пройти двумя способами).
, так как каждый цикл (1-вершина) увеличивает количество возможных путей вдвое (потому что в цикле из одной вершины в другую можно пройти двумя способами).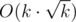 . Сначала поясним идею решения, затем покажем, как достигается такая временная оценка. Идея решения состоит в следующем. Прежде всего, если
. Сначала поясним идею решения, затем покажем, как достигается такая временная оценка. Идея решения состоит в следующем. Прежде всего, если 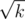 . Тогда и диагональ, которую мы рассмотрим в результате решения, описанного выше, имеет величину порядка
. Тогда и диагональ, которую мы рассмотрим в результате решения, описанного выше, имеет величину порядка 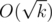 строчек и в каждой строке мы совершаем
строчек и в каждой строке мы совершаем 
