Hello CodeForces Community,
I’d like to invite you to CodeChef November Cook-Off at https://www.codechef.com/COOK64.
Time: 22nd November 2015 (2130 hrs) to 23rd November 2015 (0000 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Details: https://www.codechef.com/COOK64
Registration: You just need to have a CodeChef handle to participate. For all those, who are interested and do not have a CodeChef handle, are requested to register in order to participate.
Problem Setter: Sergii Nagin
Russian Translator: Sergii Nagin
Editorialist: Sunny Aggarwal
Problem Tester: Istvan Nagy
Mandarin Translator:: Hu Zecong
Contest Admin: Praveen Dhinwa
Vietnamese Translator: VNOI Team
Language Verifier: Rahul Arora
It promises to deliver on an interesting set of algorithmic problems with something for all.
Good Luck! Hope to see you participating!!









 точек. Тогда мы можем просто для каждой пары точек на ней (пускай они будут
точек. Тогда мы можем просто для каждой пары точек на ней (пускай они будут 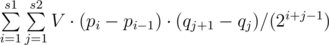 .
.
