I am happy to announce that Rocket Fuel Inc. will be hosting a Rockethon competition again! The contest is prepared by Rocket Fuel employees Eldar Bogdanov, Anton Lomonos, Lasha Lakirbaia, Alexander Ruff, Nikhil Goyal and me, Ievgen Soboliev. We hope everyone will find some interesting problems in the contest and everyone will have as much fun solving these problems as we had preparing them. Just like last year, the best participants will receive valuable prizes and top performers will get Rockethon 2015 T-shirts! Also, Rocket Fuel is interested in hiring people after this event, so please fill out the simple form during registration.
About Rocket Fuel
Rocket Fuel is building technology platform to do automatic targeting and optimization of ads across all channels — display, video, mobile and social. Our pitch to advertisers is very simple "If you can measure metrics of success of your campaign, we can optimize". We run campaigns for many large advertisers and our clients include many top companies within the following industries: autos, airlines, commercial banks, telecom, food services, insurance, etc. Examples include BMW, Pizza Hut, Brooks Running Shoes and many more!
We buy all our inventory through real time bidding on ad exchanges like Google and Yahoo. Ad exchanges are similar to stock exchanges except the commodity being traded is ad slots on web pages. Our serving systems currently process over 60B bid requests/ day with a response time requirement of 100ms. Our data platform has 64 PBs data that is used for analytics as well as modeling.
Our engineering team is still small (~150) enough for any one person like yourself to make a huge impact. The team represents many top schools in US and outside — Stanford, Carnegie Mellon, MIT, Wisconsin-Madison, IIT (India), Tsinghua (China).
Rocket Fuel has been named #4 on Forbes Most Promising Companies in America List in 2013 and #1 Fastest Growing Company in North America on Deloitte’s 2013 Tech Fast 500 and our CEO George John was recently named “Most Admired CEO” by the SF Business Times in 2014.
My Personal Story
About one year ago I visited CodeForces and saw an announcement of Rockethon 2014. My first thought was "Another competition from a big company, that's nice!". I took part in this contest, performed quite well and recruiters from Rocket Fuel have contacted me and scheduled some interviews. I passed the interviews and now I'm here, in Rocket Fuel.
It has been a nice opportunity to learn advanced concepts of software engineering from a huge amount of smart people working with you. Also, our activities here are not limited only to writing code — we do fun things here like playing basketball, soccer, table tennis. I invite everybody to take a part in the competition and would be glad to hear if any of you thinking about joining Rocket Fuel.
Contest Overview
The contest will begin on February 7, 9AM PST.
The contest length is 3 hours.
The testing of each submission will be performed as soon as the submission is received and the verdict will be delivered to the submission author right away.
The problemset will consist of 7 problems. Each problem can contain from one to three subproblems. Each subproblem will be worth a fixed amount of points. The ties between contestants with the same score will be broken by penalty time which is computed similar to ACM scoring system.
Prizes
The top three contestants will receive the following prizes:
1) IPhone 6 (16 Gb)
2) Participant can choose Apple Watch or Samsung Gear S
3) Participant can choose Apple Watch or Samsung Gear S
The top 150 performers will receive a Rockethon T-shirt designed specially for this contest.
If you are unable to take part in the competition but are interested in joining Rocket Fuel, we will be screening resumes submitted through the special form.










 , the next one —
, the next one — 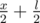 , the next —
, the next — 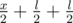 and so on.
and so on.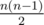 pairs of runners, then in those
pairs of runners, then in those 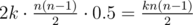 to the answer.
to the answer.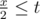 , or
, or 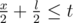 , ir
, ir 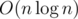 . We can reduce it using two pointers method.
. We can reduce it using two pointers method.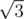 ) and
) and 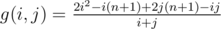 monotonically increases, so we can use moving pointer method applied to variable
monotonically increases, so we can use moving pointer method applied to variable 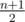 , then
, then 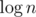 iterations with fixed
iterations with fixed  and then first go over all
and then first go over all 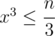 then go over all
then go over all 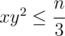 and then determine
and then determine 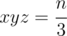 . After that we need to solve the system
. After that we need to solve the system 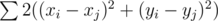 for all integer points inside the polygon or on its border. We can see that we can process Xs and Ys independently.
for all integer points inside the polygon or on its border. We can see that we can process Xs and Ys independently.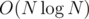 queries and add operations.
queries and add operations.


