Предлагаю обсудить задачи.
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 00:13:26 (j1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











моё решение вроде такое же. Но с бинпоиском поучало ТЛ 12. Я убрал весь STL написал свой бинпоиск и т д -> результат опять ТЛ 12. Тогда я убрал бинпоиск вообще и сделал хеш-таблицу -> ТЛ 12. Очень странно
Пихать потому что не умеете. Нужно было обычные массивы, никаких мапов и векторов.
Вообще, сортировка ведёт себя достаточно локально, а хэш-таблица страдает от кэш-промахов очень сильно. Это знание, которое, как мне кажется, стоит получать вместе с изучением сортировки и хэш-таблиц.
В соответствии с этим, после замены размера хэш-таблицы (а у вас он всё время 20 миллионов) на 218=262144, ваше самое первое решение вместо TL/9 получает TL/10, а последнее вместо TL/9 получает OK и работает за 3.9 секунды из 5 предоставленных.
С одной стороны, я понимаю, что со стороны участника неприятно придумать идею решения задачи и не сдать её из-за реализации. С другой стороны, Открытый Кубок — соревнование не по theoretical computer science, а по программированию, и единственное, что гарантируется участникам в этой связи — что решение жюри укладывается в TL как минимум дважды. Вы же не будете использовать фибоначчиевы кучи и потом говорить, что они должны были работать быстрее, потому что у них меньше асимптотика?..
Наконец, о 90% постов — голословное утверждение, приведите точную статистику.
По поводу голословных утверждений - вы еще обратите внимание, я назвал товарища JKeeJ1e30 "Грандмастером Пихания - Адептом Ордена Всезапихивания", а он таковым официально не является, то есть это тоже голословное утверждение!
Контест был супер, задачи - отличные. -N и -NN - это в основном запихивание кривых решений с не той асимптотикой. Задача A - как заметил Rizvanov (http://mirror.codeforces.com/blog/entry/2877#comment-58461), заходит даже на кривом stl, если писать правильное решение. Как написать B, чтобы не надо было пихать, написал ilyakor (http://mirror.codeforces.com/blog/entry/2877#comment-58442). Про F ничего говорить не буду - по ней куча чистых плюсов. Лично у меня заработало первое, что пришло в голову. По G - avm написал про асимптотически лучшее решение (http://mirror.codeforces.com/blog/entry/2877#comment-58531).
По-моему, когда есть несколько задач, по которым у участников есть выбор - потратить время на поиск оптимального решения или потратить время на упихивание неоптимального (и упихать) - это во многом добавляет интереса.
Я ж и говорю - крутой контест! Но я знаю несколько участников, которые в следующем году не станут тратить 5 часов своего времени и кучу невосстанавливающихся нервных клеток на ГП СПб...
В таком случае мне осталось предупредить, что седьмой этап X Открытого Кубка по плану готовит примерно тот же коллектив авторов.
И напоследок — хорошие новости: нервные клетки всё-таки восстанавливаются.
===================================================
Я считаю, что конструктивно что-то обсуждать с людьми, которые, глядя на шарик, который мне кажется желтым, говорят, что он синий - бесполезно. Тут нечего обсуждать - это разные видения мира. Я считаю что куча грязи и минусов в таблице и средний success rate по задачам 17% - это обычно неквалифицированное жюри, которое не в состоянии оценить возможности участников/сложность задач и поставить нормальные ограничения по времени. Если кто-то считает, что проблема в участниках - ради Бога. Петру и туристу со товарищи, наверное, действительно интересно.
=====================================
Товарищи авторы!
Вы, конечно, делайте задачи какие хотите, а мы, конечно, будем решать все подряд, да ещё и благодарны будем, ибо дарёному коню ну ты понел.
Замечание только такое. Задачи, где необходимо многопопыточное упихивание либо (в альтернативу ему) хорошее знание неких тонкостей языка программирования и/или устройства железа, не соответствуют политике ACM. Если авторы задач этот факт осознают и их такое положение дел устраивает, то тогда да, я умываю руки.
P.S. Хотя нет, формулировка не такая. Слово "необходимо" нужно заменить на фразу "в решении может существенно помочь", так правильнее будет.
1. А есть ли какой-нибудь пруфлинк про политику ACM, и какой конкретно этап имеется в виду (финал?)?
2. Про разницу конкретно сортировки и хэш-таблицы — не согласен, что это знание “о железе”. Большая константа у хэш-таблицы — это факт именно из теории алгоритмов, точнее, удобная для теоретика интерпретация того, что случается на практике. Точно так же, как в задачах на какие-нибудь деревья за
3. Я вообще не сторонник того, чтобы при составлении задач проводить такую границу: вот эти знания о программировании — хорошие, теоретические, на них задачу дать можно; а все остальные — плохие, некрасивые, должно быть можно сдать задачу и без них. В частности, по-моему, уметь искать самое узкое место в своей программе ничуть не менее ценно, чем, например, различать алгоритмы Форда-Беллмана и Дейкстры по асимптотике. И я считаю, что как составитель задачи вправе в какой-то момент потребовать от участников применить это умение.
4. Бывают задачи, в которых правильное по асимптотике решение работает моментально, а неправильное не проходит по времени с десятикратным запасом. Бывают задачи, в которых ограничения подобрать таким образом невозможно. Эти задачи тоже ценны.
1. Ну как, конечно же, есть. Вот про финал, там есть такое предложение: "Problem authors should assume that English is the second language of the reader, and they must thoroughly explain any culture or discipline-specific aspects". А вот и про наш полуфинал, там есть такое: "As far as possible, problems will avoid dependence on detailed knowledge of a particular applications area or particular contest language". Да и практикой подтверждается - не припомню ни одной задачи с четырёх последних NEERC, где приходилось бы что-то пропихивать, - там всегда получается так, что если асимптотика хорошая, то проходит с большим запасом, а если плохая, то никакая магия низкоуровневых оптимизаций тебе не поможет. Конкретный пример такой задачи - D с NEERC-2008, там квадрат чётко отсекается от квадрата на логарифм.
2-3. О вкусах спорить не будем. Я указал объективную причину, почему некоторого рода задачи плохи, если предполагать, что основная миссия Открытого Кубка - это как бы тренировка команд для наилучшего выступления на ACM-ICPC. Если мы этого не предполагаем (а это вполне допустимо не предполагать, ведь среди участников OpenCup много и ветеранов ACM), то тогда мой аргумент снимается.
4. Теоретически-то понятно, как делать так, чтобы проходили алгоритмы только с задуманной автором асимптотикой: поднимать ограничения на входные данные на несколько порядков, но это, конечно, довольно дорого, ведь и ограничения по времени и памяти придётся поднять. Тут мы можем только сказать, что задача отсечения асимптотически плохих решений будет решена с дальнейшим прогрессом вычислительной техники :)
1. Про финал не убедил, в этой фразе нет никакого отделения алгоритмической части решения от программирования вообще. Про полуфинал тоже фраза не совсем о том. Вот то, что практикой подтверждается, это уже гораздо больше похоже на правду.
Кстати, Пучер (кажется, в Петрозаводске) говорил о цели всех этих соревнований ACM ICPC, что они не ради самих себя, а чтобы люди учились хорошо программировать (это, конечно, моя интерпретация). Так вот к этому как раз ближе идея задач на всё что угодно, чем задач только на правильно придуманный алгоритм.
2-3. Вкусы тут ни при чём. А у OpenCup вообще не сказано, какая миссия, каждый понимает её как ему нужно. Снарк мне на такой вопрос ответил, что одна из миссий — “соревнование на контестах разных авторов, разных школ и разных стилей”.
4. Возможно, не боянами к этому моменту останутся только задачи, в которых надо отсечь
Дело в том, что я ее по некоторым причинам очень хорошо помню :-)
http://neerc.ifmo.ru/past/2008/standings-with-time.html
Так вот:
(1) Там НЕ проходил N^2log времени и N^2 памяти (см 5-е место), хотя решение с N^2log времени и N памяти проходило и считалось "правильным" (так же, как и N^2-ное решение).
(2) N^2log времени и N^2 памяти таки заталкивался (см. 3-е место :-)
==================
Если и правда заталкивался, то это печально :(
А как там можно было сделать за линию по памяти? O_o Я-то имел в виду обычный алгоритм Дейкстры с бинарным деревом.
А реализовать эту идею можно за N^2logN или N^2 времени и (в обоих случаях) N памяти.
По поводу поиска bottleneck'ов в контексте сервера opencup'а говорить очень странно - не помню, когда последний раз в "проблемной" задаче bottleneck локально и на сервере совпадал.
На самом деле проблема СПбГУ-шных контестов вовсе не в жёстких ТЛях, а в тестах, наполненных максимальными тесткейсами. Из-за этого приходится считать миллисекунды :( Не очень круто, если при 10 миллисекундах на тесткейс задача не проходит. Понятно, что это "как на финале", но на финале никогда не бывает тестов, набитых максимальными тесткейсами.
Нет, это не совсем “как на финале”, ведь там не указано, сколько точно и каких может быть кейсов.
А тут подход такой. Давайте полностью формально опишем все ограничения (количество кейсов, сумму длин всех кейсов, ...). После этого корректными будем считать те и только те решения, которые проходят все подходящие под ограничения тесты.
Соответственно, набор тестов будем считать полным, если он отсекает (на практике — старается отсекать) все неэффективные с учётом ограничений решения. Зато никаких умолчаний типа “кейсов сотни, но не тысячи”, и “больших из них всего парочка”.
Ну заводить массив большого размера и прыгать по нему рандомно 500 миллионов шагов. И с разными размерами массива сабмитить. Как только вылезете за кеш - время работы начнёт расти сильно быстрее.
Можно ещё попробовать вставить вызов CPUID и сравнивать с предполагаемым значением (типа, если 1 Mb, то сделать TL, если 2, то WA, если 4, то PE, иначе RE). Правда, в каких-нибудь judge это может быть запрещено.
Хеши быстрее сортировки, если правильно их писать. Зачем размер хеш-таблицы 20 миллионов для меня не понятно, там ведь максимум 10^5 элементов хранится.
Либо у вас неоптимальное решение (которое кладёт 20 миллионов чего-то в хеш мапу) либо не умеете писать хеш-таблицу по челевечески.
Это если бы не придумали кеш. А с ним получается такое несложное арифметическое построение. Предположим, что хеш идеальный, то есть ведёт себя как случайное число, равномерно распределённое на диапазоне.
Пусть размер кеша 1 мегабайт, и пусть он всегда заполнен элементами хеш-таблицы. Если наша хеш-таблица занимает 2 мегабайта, вероятность ткнуть мимо равна
Теперь учтём, что загрузить кусок основной памяти в кеш — это во много раз более трудоёмкая операция, чем сложить и перемножить два числа. Пусть это в среднем занимает k· T, где T — ровно столько времени, сколько занимают все нужные нам операции с одним добытым элементом хеш-таблицы.
Теперь прикинем. Если размер хеш-таблицы в 2 раза больше, чем реальное количество элементов в ней, и равен 2 мегабайтам, в среднем мы тыкаем в
Если таблица в 10 раз больше, чем количество элементов, и её размер равен 10 мегабайтам, в среднем мы тыкаем в
Видно, что чем больше k, тем второе время хуже первого.
Если бы не было этого эффекта, было бы всегда выгодно заводить хеш-таблицу на все 256 мегабайт данной в задаче памяти. Но ведь почему-то обычно так не делают...
Не буду выдумывать хитрые формулы, просто скажу из моей практики: размер хеш таблицы должен быть такой, сколько элементов ты туда добавляешь. я чаще беру степень двойки которая не меньше n. Например для 10^5 беру 1 << 17. Это выгодно ещё и тем, что не нужно операции остатка от деления, можно юзать битовые операции. x % hash_size == x & (hash_size - 1), если hash_size = 1 << k
Это количество плохих пар получается, дальше вычитаем из общего кол-ва = ответ.
Спасибо! Мне отчего-то взбрело в голову, что Вы находите все делители.
Аналогичная проблема :(
Если коротко. Заметим, что у нас есть некоторое полное двоичное дерево высоты L, каждой букве соответствует некоторая вершина дерева, ни одна из букв в таком дереве не является потомком другой. Тогда если буква расположена на высоте h, то она "съедает" 2^(L-h) листьев. Заметим, что код можно построить тогда и только тогда, когда sum(2^(L-h[i])) <= 2^L. Тогда можно написать тупую динамику: dp[i][j] - ответ, если мы закодировали уже i букв и потратили j листьев. Проблема лишь в том, что j может быть до 2^L, т.е. примерно до 10^9.
Сделаем следующее. Посортим все буквы по возрастанию кол-ва использований. Тогда длины их кодов будут невозрастать. Поэтому если у нас есть буква с кодом длины h, т.е. съевшая 2^(L-h) листьев, то количество листьев, потраченных на предыдущие буквы, можно округлить вверх до числа, кратного 2^(L-h). Тогда получаем такую динамику: dp[i][j][k] - ответ, если мы закодировали i букв, у последней длина кода - j, и всего потрачено листьев k*2^(L-j). Пересчитывается она за константу, и с большим скрипом влезает в tl.
Нам не хватило осознания того факта, что можно округлить.
кто-нибудь знает, как решается I ?
Идея примерно такая же. Будем генерировать случайные лабиринты по алгоритму и сортировать их по расстоянию до цели.
Как только лабиринтов стало много (скажем, 10000), берём тот из них, до которого расстояние минимально, и проходим его (естественно, сдвигаясь так же во всех остальных и во всех будущих лабиринтах). После этого догенерируем ещё лабиринтов так, чтобы у нас висело 10000 непройденных, и опять пройдём тот, который быстрее всего пройти. Будем повторять, пока не кончится длина ответа. Это уже где-то 1000–1100 штрафа.
Улучшение: при равенстве расстояний (а после первых нескольких лабиринтов минимальное расстояние будет почти всегда 1, и будут сотни лабиринтов на таком расстоянии) выбираем шаг в ту сторону, в которую лабиринтов за этот шаг пройдётся больше. Это важно: сразу становится 700–800 штрафа.
Ещё нужно, чтобы генератор работал быстро (например, в поиске двух наиболее удалённых клеток притворимся, что граф — дерево), так как с такими константами генерируются миллионы лабиринтов, а длина ответа всё не становится 10000.
Константы (размер поддерживаемого множества и желаемую длину ответа) можно подкрутить так, чтобы и работало минут 5–10, и штраф был 800–900.
Ещё я пробовал генетический алгоритм, который строит ответ по маленьким кусочкам длины 100 (здесь и далее в решении все константы взяты с потолка). Для каждого кусочка сгенерируем 1000 лабиринтов и будем оценивать ответы по тому, сколько из них пройдено. Популяция — 100 путей, сначала просто пишем случайные буквы. Скрещивание — начало и 50 от одного + 50 от другого, мутация — какие-то символы ответа заменить на прохождение с этого места какого-нибудь лабиринта. Сгенерировали несколько поколений, 100 лучших кусочков зафиксировали как начала путей и с ними аналогично строим 101..200 символы ответа, и так далее.
Правда, этот алгоритм часа за полтора с трудом добивается штрафа 830–960, но в реализации есть что улучшить.
Как пихать B?
+
В итоге написали мнговенно работающее решение с КТО. Найдём ответ по модулям 65535 и 65537. Как же это сделать? Пусть ответ n,
что ты понимаешь под meet-in-the-middle относительно этой задачи?
giant-step-baby-step?
я запомнил в хеш таблице для всех 0 <= i < (1 << 16), map[(X^(i << 16)] = i;
потом домножал A на X и искал это в таблице.
на C++ с самописной хеш-таблицей прошло спокойно.
Есть подозрение, что у нас тормозил вовсе не поиск (который хоть и двоичный поиск, но всего с 1-2 промахами кеша), а умножение многочленов по модулю. Но это фиг поймёшь - на нашем компе на 500 кейсах работало полсекунды, но он 1) 64-битный, 2) с большим кешом.
а как делали умножение и остаток? я многочлен в long long хранил.
умножение за ~32 битовых операции с ними и остаток тоже.
Кстати, при аккуратной реализации всё в 32-битный целый тип помещалось.
Не знаю, на сколько это быстрее long long'ов, но думаю, что хоть немного, но тоже ускоряет.
Нам помог __gnu_cxx::hash_map. В meet-in-the-middle били степень на 2 одинаковые части.
стратегия для 1го игрока: если есть нечетный делитель n, то возьмем такой наименьший (скажем, k) и периодом k закрасим вершины 1м ходом. тогда все оставшиеся вершины развалятся на циклы длины n/k с периодом k. несложно показать, что теперь при любом ходе мы будем закрашивать вершины только в одном из таких циклов. ну и все - первый игрок для себя делит оставшиеся циклы на пары и симметрично повторяет ходы второго игрока.
если начетного делителя нет, то n=2^x. по сути все вершины можно разбить на 2 цикла в периодом 2 и они будут работать как и в 1м случае. тут 2й игрок пользуется вышеописанной стратегией 1го игрока.
ну и еще случай когда ходов вообще делать нельзя (n простое) тривиален - тут выигрывает 2й игрок.
Во-вторых, по правилам OEIS пользоваться было нельзя.
Хотя при таком решении ответ на вопрос “кто выиграет при правильной игре, начиная с пустой доски” будет такой же: проигрышные партии так и остались проигрышными, а в выигрышных нам важно, чтобы был такой ход, что
Значит мое решение, которое я писал на контесте, (а оно разбило бы именно так) неверно. Что характерно, прошло 19 тестов, а на 20-м упало по времени.
Решение-то может и неверно, но ответ у него верный :) . Косвенное подтверждение — до этого места есть все тесты 1001..2000.
А как люди решали C? У нас была идея приблизить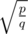 дробью
дробью 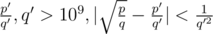 (просто цепной дробью), а после этого считать количество целых точек q'y - p'x > 0. Но для этого надо уметь решать полученную задачу, что вроде бы баян, но само по себе сложно. Она так делается и все умеют писать решение для ax + by > 0 по памяти, или тут что-то проще?
(просто цепной дробью), а после этого считать количество целых точек q'y - p'x > 0. Но для этого надо уметь решать полученную задачу, что вроде бы баян, но само по себе сложно. Она так делается и все умеют писать решение для ax + by > 0 по памяти, или тут что-то проще?
Сначала нужно из префиксной записи сделать нормальную, а затем из нормальной сделать постфиксную.
Если текущий символ (обозначим его с) - плюс или минус, вызовем функцию еще 2 раза подряд (т.е. для операндов этого оператора) - получим строки s и t, и возвратим s + t + c.
Иначе возвращаем c.
Яндекс.Тренировки (логин пасс опенковский).