Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 160 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
| Название |
|---|



Can't understand C's explanation.
For maintaining minimal alphabetic letter in current string $$$s$$$ there's enough to precalc $$$ms_i$$$ — minimal letter for each suffix of $$$s$$$. Minimum on suffix starting from position $$$i$$$: $$$ms_i = min(s_i, ms_{i+1})$$$. This way is faster: just $$$O(n)$$$.
Before adding to stack a letter at position $$$i$$$, while letter in the top of the stack is not greater than minimum on suffix starting from position i, pop the letter from the stack and add it to the answer.
Alternately F can be solved with Divide and Conquer Optimisation as well.
I seem to get TLE with Divide and Conquer Optimization , was any pruning required to pass the time limit ?
It's Complexity O(n^2logn)?
Ввиду того, что в задаче F норок всего
5000, а их вместимость не более5000, то можно просто заменить их на25 * 10^6и решать задачу, что в каждую норку максимум может влезть одна мышь. Это уже более стандартная динамика,dp[i][j]—iмышь бежит в норкуjпри условии, чтоi-1бежала максимум в норкуj-1. Единственное исключение — то, что не нужно пытаться засунуть каждую мышь в каждую норку, а только в5000норок слева или справа от позиции мыши, поэтому вторая размерность динамики будет равна10000, а не количеству норок. Дополнительно следует хранить соответствие вторых индексов динамики и номеров норок. Чтобы быстро прибавлять ответ с предыдущего слоя, хватит и частичных минимумов. Также, для каждой мыши потребуется найти ближайшую слева норку, например, бинарным поиском. И, возможно, потребуется хранить только два слоя динамики для оптимизации по памяти.Problem E can also be solved offline with an O(n) memory complexity, by sorting the queries w.r.t k and solving all queries with the same k together using dynamic programming.
Intuitions about the time complexity:
I don't know exactly how to calculate a generalized upper bound for the time complexity, but I had the intuition that it would fit in time using this approach
Implementation: 26497630
(1/2 + 1/3 + 1/4 + ... + 1/n) = O(logn)
Oh yes you're right, it's logn. I got confused about it. Thanks.
dropped
Note, it's order.
Hint for proof: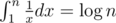
I didn't learn integrals in school yet. But I could see that your formula is not correct:
Seems that functions are crossing and lying nearby but not equal.
click
Actually, it's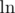 not
not 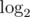 . And you can see that the difference between
. And you can see that the difference between 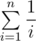 (a.k.a harmonic number) and
(a.k.a harmonic number) and 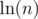 go smaller as n go bigger. It will eventually equal 0 when n big enough. Furthermore,
go smaller as n go bigger. It will eventually equal 0 when n big enough. Furthermore, 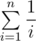 is smaller than
is smaller than 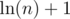 and as we can ignore constant, we can say it's O(logn)
and as we can ignore constant, we can say it's O(logn)
Thank you, I thought
logalways meanslog2in informatics, notln.Here is another proof: 1/1+1/2+1/3+1/4+1/5+1/6+1/7+..<1/1+1/2+1/2+1/4+1/4+1/4<1+1+1...+1=log n and 1/1+1/2+1/3+1/4+1/5+1/6+1/7+1/8. <1+1/2+1/4+1/4+1/8+1/8+1/8+1/8<1+1/2+1/2...+1/2=log n/2 So 1/1+1/2+...+1/n is O(log n)
But the time is worse than using sqrt precalculation..
Look, if all k will be different your code will make this Q times:
memset(dp, -1, sizeof(dp));It is optimized of course but making your complexity bigger.Sorry for necropost, but in this case your solution works in
O(n sqrt(n))time:Because your solution takes O(n) operations per one block, but this is O(n) memory, u are right
hi excuse me but if all queries have different k's then you say if (k != prev) {memset(dp, -1, sizeof(dp));} so you basically fill the dp with -1's in every query but isn't this O(n^2)? could you explain why you don't get TLE? thanks ,and sorry to bothering you :D
I understand that this contest is quite old but 797C - Minimal string has a typo and says "lexigraphically" instead of "lexicographically". I'm not sure if this is correct way to report typos but don't see any other.
Fixed, thanks.
Can anyone give me a DP solution for Problem B? Why is this approach wrong?
Here is the DP solution in case you need it still.
http://mirror.codeforces.com/contest/797/submission/41646680
Can anyone tell me where am I wrong in this code. It is giving wrong answer for an input. I am not getting why my code is giving wrong output for that input. Printing o before n. http://mirror.codeforces.com/contest/797/submission/33380771
can anyone can give me some test cases on the question C I am getting WA at test 21?
test this maybe it would help :D
input: czzbaz output should be: abzzcz
Yeah mate, really helpful test case. After testing with this one got AC
Someone please explain problem 797F . Can't understand the editorial!!!
someone please simulate this case:
acdb
s = acbd, t = '', u =''
s = cbd, t = a, u = ''
s = bd, t = ca, u = '' [first char 'c' was taken and string t was appended]
s = b, t = dca, u = ''
if the last character is to be extracted from t then it is 'a' and it will be in the last position of u which is not the output given in the test case.
i think i am misinterpreting the following lines
"Extract the first character of s and append t with this character.
Extract the last character of t and append u with this character."
Problem statement of C is very misleading. At first I could visualize string T nothing more than a queue and sorting seemed impossible.
problem c at first i had difficulty understanding the question and then with whatever i understood ,i wrote a dp solution but it got WA on TC 17.if anyone has dp solution or can find the error in my code , it will be helpful.96818512 is my submission.
try this test case: eeddcbeeec
correct ans is: bcceeeddee while your code gives: bceeecddee
HI, can anyone help me to provide the time complexity of my solution to problem E,
Here is the link to my submission:- https://mirror.codeforces.com/contest/797/submission/100305884
I guess it is n√n,
I have solved for every k individually and for a particular k, i have solved for all different values of p and storing the result for traversed indices for every p.
I think that worst case complexity would be, n + 2*(n/2) + 3* (n/3) + ... x terms s.t. x*(x+1)/2 = q; Because as k increase from 1 to n I can solve for particular k and pparticular p in n/k time, so, if all k are different then it will be, n + n/2+n/3... = nlog(n), and if there are multiple p for same k then it will be (dup, no.of different p for same k), (n/k * min(dup,k)).
In problem C the statement is completely wrong. It should be:
Move1: Extract the first character of s and append this character with t.
Move2: Extract the last character of t and append this character with u.