TooDumbToWin's blog

ICM Technex 2018 and Codeforces Round #463 (Div. 1 + Div. 2, combined)

By TooDumbToWin, 7 years ago, In English

Hello, Codeforces!

I would like to invite you all to the International Coding Marathon 2018, under the banner of Technex'18, IIT (BHU) Varanasi. It will take place on Thursday 15th February 2018, 20:05 IST. The contest will be held as a combined Div.1+Div.2 round which will be rated for participants from both divisions.

The problemset has been prepared by me (TooDumbToWin), DeshiBasara, hitman623, dhirajfx3, karansiwach360 and Enigma27. We would like to express our heartiest thanks to vintage_Vlad_Makeev and KAN for their constant help in preparing the contest and MikeMirzayanov for the amazing Codeforces and Polygon platforms. We also thank AlexFetisov and winger for their invaluable help in testing the problems.

Prizes

  • Overall 1st place: INR 35,000
  • Overall 2nd place: INR 25,000
  • Overall 3rd place: INR 15,000
  • 1st place in India: INR 10,000
  • 2nd place in India: INR 8,000
  • 3rd place in India: INR 6,000
  • 1st place among IIT (BHU) Varanasi freshmen: INR 1,000

Participants will have 2 hours to solve 7 problems. The scoring distribution will be announced soon.

Good luck everyone! Hope to see you on the leaderboard.

Update: Scoring is 500 — 1000 — 1500 — 2000 — 2500 — 2500 — 3000

Update 2: Thanks to all participants and congratulations to all the winners. The winners, who are eligible for prizes, will soon be contacted regarding the same.

Overall top 10

  1. Radewoosh
  2. fateice
  3. Um_nik
  4. laofudasuan
  5. dotorya
  6. 300iq
  7. LHiC
  8. ksun48
  9. wxh010910
  10. chemthan

Indian top 5

  1. PrashantM
  2. rajat1603
  3. Baba
  4. jtnydv25
  5. adkroxx

Some problem statements were not clear. We deeply regret the inconvenience caused.

The editorial has been posted here. This was first contest set by most of us, so please help us do better next time by filling this form.

  • Vote: I like it
  • +261
  • Vote: I do not like it

Comments Comments (158)
| Write comment?
»
7 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Is this like IIT BHU's contest — Manthan ?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +29 Vote: I do not like it

    The only difference is Manthan is an event of Codefest, the annual coding festival of Computer Science and Eng. Dept. of IIT BHU while ICM is an event of Technex, the annual techno-management fest of our Institute.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +26 Vote: I do not like it

      Oh, I see .. so the same people are organising ?

      In Manthan, I enjoyed problem B - Marvolo's Gaunt Ring a lot — It had two beautiful solutions.

      I hope this contest is just as good as the previous ones !

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +15 Vote: I do not like it

        Yes, the same people are organising it.

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +46 Vote: I do not like it

        I hope it's better...

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +1 Vote: I do not like it

          If you wanna win prize you should be Legendary Grandmaster or Indian )))

          → Reply
»
7 years ago, # |
  Vote: I like it +13 Vote: I do not like it

Here is the link to the previous ICM Technex 2017 and Codeforces Round #400 (Div. 1 + Div. 2, combined)

→ Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

What is INR?

→ Reply
»
7 years ago, # |
  Vote: I like it +2 Vote: I do not like it

2nd rated contest in 2 days, YaY

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +26 Vote: I do not like it

    This is 2nd of 4 rated contests(for Div. 2) in 4 consecutive days.

    → Reply
»
7 years ago, # |
  Vote: I like it +12 Vote: I do not like it

Can I say that happy Lunar New Year ……

→ Reply
»
7 years ago, # |
  Vote: I like it +14 Vote: I do not like it

Will it be a hackforces？

→ Reply
»
7 years ago, # |
  Vote: I like it +33 Vote: I do not like it

After the disaster yesterday where I failed systest on two problems (the pretests are really too weak), I decided to skip the Chinese New Year celebration and try to get my rating back on this one. Good luck everyone.

→ Reply
»
7 years ago, # |
  Vote: I like it +62 Vote: I do not like it

In my timezone, the contest will end at 23:35, so I could enjoy both of them :D.

a_1_1

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it -39 Vote: I do not like it

deleted

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Atleast 2 hours 30 min contest would have been better since there are 7 questions to solve.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    On the bright side, if you get stuck on a question, there will be another one of roughly the same difficulty.

    If you take a look at last year's contest, it was 7 problems in 130 minutes. I did a virtual of it and it seemed pretty appropriate.

    → Reply
»
7 years ago, # |
  Vote: I like it +9 Vote: I do not like it

I have one question TooDumbToWin. If Indian user get 1'st place at Overall, so it says that he(she) is 1'st plase in India. He(She) get INR 35,000 + INR 15,000?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +41 Vote: I do not like it

    Every winner will get only one prize. If he's first overall and first in India, he will get the first overall prize and the second place in India will get the first and so on.

    → Reply
»
7 years ago, # |
  Vote: I like it +7 Vote: I do not like it

I can't de-register myself from the contest. I get a pop-up saying that I've at least made one action in the contest. (I really don't know whats this suppose to mean). I just hope it's not rated for me!

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Just don't submit in the contest and it won't be rated for you. :)

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +7 Vote: I do not like it

    UPDATE- I'm able to de register now.

    → Reply
»
7 years ago, # |
  Vote: I like it +60 Vote: I do not like it

Feels like tourist is coming, cause of Um_nik's danger *_*

→ Reply
»
7 years ago, # |
  Vote: I like it +83 Vote: I do not like it

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by TooDumbToWin (previous revision, new revision, compare).

→ Reply
»
7 years ago, # |
  Vote: I like it -23 Vote: I do not like it

Contest prepared by Indians means, It's going to be Mathematical .

→ Reply
»
7 years ago, # |
  Vote: I like it -14 Vote: I do not like it

rating-=INF;

→ Reply
»
7 years ago, # |
  Vote: I like it -36 Vote: I do not like it

Jai Hind!

→ Reply
»
7 years ago, # |
  Vote: I like it +14 Vote: I do not like it

One of problemsetters is enigma27, contest will be with hacks (-_-)

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    @enigma27 see this :P

    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +9 Vote: I do not like it

    why do you think so?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +73 Vote: I do not like it

      During the Second World War the Germans used the encryption machine Enigma, which was hacked :D

      → Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

rating predictor started working

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +27 Vote: I do not like it

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +76 Vote: I do not like it

A confirmed cheater — .Ali. and his clone Ali_Pi. Shame on you!

UPD: Disqualified — only in 3 minutes. Thanks (anyone) for being so incredibly responsive.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How did he manage to generate all those hackable solutions ?

    Respect

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +9 Vote: I do not like it

      maybe ... 

      if (a==1&&b==2) print a wrong answer;
      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Never think about it. Thank for sharing :D

        → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it +9 Vote: I do not like it

      More importantly how he managed to be in the same room? isn't that random?

      edit: if you have many accounts, then its like the birthday paradox where you don't need too many accounts

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    How these two users can enter the same room？

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      It's kind of luck. Perhaps there is a way to manipulate, but I have no heart to look up for it... ;)

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it +34 Vote: I do not like it

        Estimate the number of rooms using number of registrants. Let it be n. Create n + 1 fake accounts. It is guaranteed that there will be atleast one of his fake account in his room :P

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I agree.

        → Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

How to solve E?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    i used stirling number of second kind. Let's denote S[i, j] as the stirling number of second kind. And make array B, so that B[i]=(2^(n-i))*n*(n-1)*...*(n-i+1) So, for example, B[0]=2^n, B[1]=n*(2^(n-1)), etc... Now, the answer we are finding is sum(i=0 to n) (nCi)*i^k, which is equal to sum (i=0 to k) (B[i]*S[k][i]). (Because of mathematical reason!) You can calculate this in proper time limit.

    Sorry for my bad english... have a nice day!

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    A very nice solution is you can calculate (1 + x) ^ n with Newton's Binomial, differentiate both sides (with respect to x) k times and then consider x = 1 to get the answer for k. (Write it down on paper for k = 1 and k = 2 and you'll see how it works)

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      where can i study this technique?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I'm not sure about a source but on the wikipedia page for "Binomial Coefficient", this technique is mentioned for being used to calculate the answer for this problem for the particular case of K = 2.

        → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +64 Vote: I do not like it

As I cannot participate, because I'm at school, I decided to write a short editorial to some of the problems (and also the current class is really boring and I don't have anything better to do).

Lets begin with D.

The main idea is that we will use binary lifting. Twice. Let's consider the following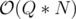 algorithm — for every vertex u (when inserted) find the closest vertex v above it with w[v] ≥ w[u]. Lets have an array nxt[], such that nxt[u] = v. Then the query will be done by simply jumping to the vertex in nxt[], until our sum becomes larger than X. Obviously this is = .

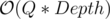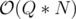To speed it up, we will have 2 binary liftings. The first on will be for finding the nxt[] and the second one will be for answering the queries. For the first one we will store the 2i-th parent and the maximum weight on the path and for the second one, we will store the 2i-th nxt[] vertex and the sum of the weights on the path. Well that's all and in such a way you can achieve .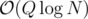

Now let's continue with F (idk why this problem is F...) .

The main idea is to use CHT. Lets have dp[u] — answer for vertex u. Obviously dp[u] = min(dp[v] + a[u] * b[v]) for every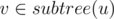 . From here we get the straightforward 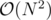solution. To get a normal solution, we simply notice that dp[v] + a[u] * b[v] is a linear function for a[u]. Well then we need to simply maintain a Convex hull trick, for every subtree. For this we will have DSU on tree. We can either use dynamic CHT or LiChao segment tree for maintaining the lines (LiChao will be much faster, as all X's on which we query are small integers). The overall complexity is .

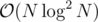It also can be solved by doing DFS order, and then segment tree of CHTs in each node on it. The complexity again is .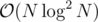

Well the round just ended I won't explain my idea for E, and it will be only F and D.

PS: How to solve G?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    I didn't solve it but I think the idea is let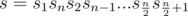 and calculate the number of ways to partition s into even-length palindromes, and then use some propogation on palindromic tree (which unfortunately I'm not familiar with).

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      I had the same initial observation, but I have no idea how to do the part with finding the number of palindromic partitions. I would really appreciate if someone explains it.

      → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Problem D i did a solution using persitents + dynamic segment tree (one tree for calculating sum, another for calculating maximum). Mine seem correct although i didn't finish it in time

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      Yes, this was the solution when problem was made but intended solution uses binary lifting which is much easier.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        Is it like spare table? I was confused because i believed that spare table can only be built with static data.

        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    for D, query type 2: number of nodes weight[R] >= weight [ (R -> parent[R] -> parent[parent[R]] -> .... -> 1) ], did i understand correctly?

    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    D: why is it optimal to take closest v above with w[v] ≥ w[u], when there could be many more nodes xi above with lower weight w[v] > w[xi] ≥ w[u] that we can now not take anymore because of weight constraint?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it +5 Vote: I do not like it

      It will be illegal because there mustn't be untaken node which is fatter than taken node (path from V0 to root)

      → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it -8 Vote: I do not like it

    Let weights of nodes be [5,4,3,7,2] So nxt[5] = 4 because node 4 is closest to 5 and w[4] > w[5](7>2) but isn't the optimal ans is sequence {5,3,2,1} so shouldn't nxt[5] = 3?

    → Reply
»
7 years ago, # |
  Vote: I like it +38 Vote: I do not like it

E
Observe answer is 2n - k·f(n) where f(n) is a polynomial of degree k.
Calculate answer for small values of n and Lagrange interpolate.
Is this expected solution?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +24 Vote: I do not like it

    No

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    I think u just need to differentiate and multiply by x the generating function (1 + x)N K times, and then just evaluate at x = 1.

    For example, for K = 2, we differentiate , then multiply by x, then differentiate again and then multiply by x again.

    I think if ur a math guy, this problem is really basic.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I came to this, too. Couldn't manage to implement it though.

      How would one go about doing the differentiation and storing the combination of polynomials and exponentials?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +20 Vote: I do not like it

        All the intermediate polynomials u will get can be expressed as xa(1 + x)b. One can use dynamic programming to calculate the answer.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Aaah ok, dp[a][b] stores the coefficient of xa(1 + x)b, and go from there.

          Was this the intended solution, or was the one with the Stirling numbers the intended solution (or both)? Either way, nice problem!

          → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      it'd be nice if you could share some links about these methods.

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Well, as it said in oeis.org: "The closed form comes from starting with (1+x)^n and repeatedly differentiating and multiplying by x", And finally replace x by 1. I could't finished the implementation in time.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    It is possible to write ik as the sum of binomial coefficients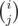 for j ≤ k. (see here for explicit formula).

    Then, we just need to solve the problem for when ik is replaced by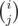 , which is doable with a simple combinatorial argument.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +20 Vote: I do not like it

    The other solutions seem too ugly for such an obvious problem so I'll share mine as well. The answer is number of ways to choose some subset of {1, .., n} and write a string of length k with elements of it. Let's first choose a string of length k and then choose some subset containing all characters of it.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +38 Vote: I do not like it

    I have another approach and I think it's beautiful!

    The answer is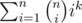 . It's the number of ways to choose a non-empty team out of n participants, and then distribute k different marbles between the team members.

    This could be done in another order: First, choose the participants who get marble and add them to the team, then distribute the marbles between them and then choose an arbitrary subset of other participants and add them to the team. Counting the number of ways to do that in this order is easy, you can find the details in my submission: 35312404

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      Can you please explain what does f[n][j] stand for in your code?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +11 Vote: I do not like it

        It is the number of ways to distribute n different marbles between j participants such that every participant gets at least one marble.

        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The problem is to find:

    Break into two sums and use the binomial expansion of (r + 1)^(k - 1) to show that

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I solved it using a recurrence which is:

    f(n,k)=n*(f(n,k-1)-f(n-1,k-1))

    Its pretty easy to derive this. :)

    → Reply
»
7 years ago, # |
  Vote: I like it +26 Vote: I do not like it

What is pretest 6 in F?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +61 Vote: I do not like it

    There is an overflow issue in your code. B * M would overflow long long and you should convert to double for comparison. This is in the standard Dynamic CHT implementation.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Another math contest...

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +37 Vote: I do not like it

I'm only 1min away from getting F correct. I found the mistake when there was only 42sec left. I'm so pissed now. I am trying really hard not to cuss.

PS: I literally threw my mouse in rage.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    I was clicking on submit on E with 2 seconds left. Tell me about it.

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +16 Vote: I do not like it

I literally was submitting (probably) correct E at the last second ... and didn't make it!

EDIT: Luckily I got TLE at test 19. Everything's fine.

→ Reply
»
7 years ago, # |
  Vote: I like it +62 Vote: I do not like it

It took me 30 minutes and 3 clarification to understand D. Am I the only one who have trouble with statement of this problem?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    no

    I've your problem too :(

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Same bro. After the second public clarification, I gave up all hopes of solving D. Started to look for E, but not enough Math knowledge to break it.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +7 Vote: I do not like it

    Codeforces is now a place to practice our reading and googling skills.

    → Reply
»
7 years ago, # |
  Vote: I like it -20 Vote: I do not like it

i don't like this contest at all ...

feel stupid for participating in the round ...

→ Reply
»
7 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Any corner cases in C?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    i was checking whether gcd of a,b divides n.. if it does answer always exist.. this is where i was wrong.. in ax+by=n x and y can be negative but they cannot be here.. costed me 6 wrong submissions :(

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I was also stuck to find non-negative solution to ax+by=n.It was very late to realise that n is 1e6 and we can find it in O(n)

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Someone please explain me problem C.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it +4 Vote: I do not like it

    In c we have to first check if any non negative integral solution exists to the equation ax+by=n;
    if not then print -1;
    else lets say a*x1+b*y1=n;
    you have to x1 cycles of length a and y1 cycles of length b.That's all i think.
    In the cycle edges will be between i to p[i]

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I solved it that way, and got a TLE in pretest 8.

      Is the usual way of outputting each integer one-by-one (by cout/printf) not fast enough?

      EDIT: If anyone still cares, turns out the problem with the code I submitted during the contest was quite subtle: there's an integer overflow I did not notice, i.e. probably not related to speed of output.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        Printf should be fast enough.

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        I guess in c++ people usually two lines of code in starting of their main function.

        ios_base::sync_with_stdio(0);
cin.tie(0);
        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You can make a small draft on the 1st pretest based on what the problem gave you. You will figure out: if g(i) = A, the i-th number of the permutation is within a loop of A element(s).

    Like, in the permutation [2, 3, 4, 5, 1], surely g(i) = 5 for all members, as:

    f(2, 1) = 3

    f(2, 2) = f(3, 1) = 4

    f(2, 3) = f(3, 2) = f(4, 1) = 5

    f(2, 4) = f(3, 3) = f(4, 2) = f(5, 1) = 1

    f(2, 5) = f(3, 4) = f(4, 3) = f(5, 2) = f(1, 1) = 2

    Similar to all other numbers.

    So, all N members must be divided in a way that there are x cycles of size A, and y cycles of size B (x and y are non-negative integers, and x*A + y*B must equals exactly N).

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      i figured that out during the contest, but i didn't know how to check that N=x*A+y*B has a solution where x,y are non negative integers

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        At first, initialize x and y with the value of -1.

        You can run a loop of integer i from 0 to N div A:

        If N - i * A is divisible to B, then a solution is found. Set x = i and y = (N - i * A) / B and break the loop.

        After the loop, if no solution is found (x and y are still equals to -1, that means there is no solution), output "-1" and terminate the program.

        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Think about it like this. The problem asks you to choose a permutation P so that if you do i=P[i] A/B times i gets its initial value. For instance if A is 3, and P={2,3,1} if you apply the operation 3 times for i=1, it becomes 1 again. If you think about it, if you apply that operation on i A/B times and it becomes i in the end, then so will applying the operation A/B times on P[i], or P[P[i]]. You can think of it as a graph, with an edge from i to P[i]. So in the end you have to make cycles of length either A or B.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It came to my mind during the contest, corrrect me please: I thought that the answer will be always P=[1 2 3 ... n] . Suppose x = min(A,B), so in x moves this permutation will always satisfy both function f and g.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I didn't think about it that way but yes, I think you're right.

        → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +21 Vote: I do not like it

Is G kind of similar to this problem: http://mirror.codeforces.com/contest/906/problem/E ? (Here, we want to count rather than find min).

→ Reply
»
7 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

Anyone else got TLE in pretest 8 of problem C? How to solve it fast enough, and do we need an output method faster than outputting each integer one-by-one by cout/printf?

EDIT: If anyone still cares, turns out the problem with the code I submitted during the contest was quite subtle: there's an integer overflow I did not notice, i.e. probably not related to speed of output.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hey man I saw your code and it looked fine. Maybe add the space and integer within a single printf? that might be faster.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    I think it might due to the gcd, but I don't know why.

    I use the same method and get RE on pretest 8.

    Finally, I found that it doesn't need to use gcd to solve something like ax+by=gcd(a, b), we could just enumerate x, then I got AC.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What the problem number C said,i didn't understand.Anyone please explain .

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You can make a small draft on the 1st pretest based on what the problem gave you. You will figure out: if g(i) = A, the i-th number of the permutation is within a loop of A element(s).

    Like, in the permutation [2, 3, 4, 5, 1], surely g(i) = 5 for all members, as:

    f(2, 1) = 3

    f(2, 2) = f(3, 1) = 4

    f(2, 3) = f(3, 2) = f(4, 1) = 5

    f(2, 4) = f(3, 3) = f(4, 2) = f(5, 1) = 1

    f(2, 5) = f(3, 4) = f(4, 3) = f(5, 2) = f(1, 1) = 2

    Similar to all other numbers.

    So, all N members must be divided in a way that there are x cycles of size A, and y cycles of size B (x and y are non-negative integers, and x*A + y*B must equals exactly N).

    → Reply
»
7 years ago, # |
  Vote: I like it +15 Vote: I do not like it

Unable to enter the Contest.Is any one facing the same problem

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    Strangely enough, the standings site works quite fine. All other sections of the contest site failed to load.

    → Reply
»
7 years ago, # |
  Vote: I like it -6 Vote: I do not like it

nice contest and good problems:)

→ Reply
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

I love clear and concise statements. Great contest!

→ Reply
»
7 years ago, # |
  Vote: I like it +34 Vote: I do not like it

Can E be solved in O(k*log^2(k)) with some FFTs?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    Yes, in O(k log(k)) using FFT. The idea of stirling numbers is same as in this problem

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      But precision issues 109 + 7 ?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +22 Vote: I do not like it

        No, precision issues can be easily avoided. See idea in this blog. Polynomial multiplication which uses exactly 3 fft calls exists that can find answer modulo any number (not only primes) less than 230.

        → Reply
»
7 years ago, # |
← Rev. 5   Vote: I like it +19 Vote: I do not like it

I've seen lots of DP approaches for problem E (I didn't understand it yet). However I want to share my approach heavily based on math.

It's not so hard to see that we want to calculate smth like: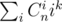

Let's start from well known formula:

Now we know it's polynomial of x. Let's differentiate it:

. Let's denote it as (1).

Substituting x = 1 gives us:

. Let's denote it as (2).

Let's differentiate (1) one more time and set x = 1. We'll get:

. Let's call this equality as (3).

Summing (2) and (3) we'll get:

and so on and so on.

The only thing we are left with is to code :) Link to submission: link

P.S. I would be pleased if someone could explain DP approach.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it +5 Vote: I do not like it

    BTW, discussing this approach with Ancient_mage he gave another hint.

    We now know that our answer is in form 2n - k * P(x) where deg of P(x) is exactly k. So we can easily interpolate it in runtime calculating values of P(x) at k points straightforward.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    how did you get the idea of differentiating and substituting x = 1?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I feel like it's standard thing when you want to crack some combinatoric formulas :)

      → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it +3 Vote: I do not like it

    mentioned above, but my comment seems to be helpful for you.

    I'm not good at coding this part : 'and so on and so on'

    So I used more mathematical technique.

    Let's denote 2n = B[0]

    n × 2n - 1 = B[1]

    n(n - 1) × 2n - 2 = B[2]

    ...

    so that B[i] = 2n - i × n × (n - 1) × ... × (n - i + 1)

    Now, i calculated stirling numbers using dp, since it has the recurrence relation : S(n + 1, k) = k × S(n, k) + S(n, k - 1)

    And then, to calculate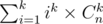 , we just need to calculate 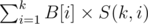, because of famous formula of stirling number (of course second kind).

    I hope my comment helped you. Sorry for my bad english. Have a nice day!

    UPD: thanks for your help! Now I get to know how to type cleaner :)

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Thank you, now I got dp approach:) You can use TeX format embracing text with dollar sign.

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I am very curious about why did i_love_you_bangladesh’s attempts on F and G were ignored. P.S. I have seen during the contest that his G passed pretests

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

TFW in D I have an if for the case to output 0 and I do not update the last...

→ Reply
»
7 years ago, # |
← Rev. 4   Vote: I like it +85 Vote: I do not like it

All I did in Problem E was to google whether there exists some formula to compute the obvious summation. Within a couple of minutes I found this link and directly copied the Using Stirling Numbers summation mentioned in the second answer.
It is sad to see that such (very easily) googlable problems are present as hard problems. I wonder how the testers did not think about checking whether such a thing is easily available online or not.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +56 Vote: I do not like it

    How to make a contest?

    Leave first 3 problems.

    Make an ok D problem, but make it harder by twisting the statements so that it is difficult to parse.

    Copy problem E.

    Make an obvious problem F.

    Again copy idea of problem G from Div1 E (atleast you accepted it above).

    Best part give less time to participants for the problem so that it looks less people were able to solve your harder problems and your contest looks good. Huh!, when will you make good contest? I generally give up seeing contest like this.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it -14 Vote: I do not like it

      It takes a lot of hardwork to create problems, so we should praise their hardwork. That is what I think.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +60 Vote: I do not like it

        Yeah, it takes a lot of hardwork to create problems, but it doesn't take so much to copy them.

        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +21 Vote: I do not like it

    I also was amazed after seeing that because kevinsogo discussed it in the IPC camp. And with two setters in the camp,then I thought may be it was intendedly made around the concept of that formula.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    F just combining convex-hull-trick and smaller to large (very innovative idea) and G some observation from another problem and its reduction to a discussed problem several times (also very innovative).

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +39 Vote: I do not like it

    This problem was my idea and I agree I should have checked the problem on Google before adding it. Apologies.

    → Reply
»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

932E - Team Work So now I have to search over research papers for combinatoric summation formulas over the internet to solve a problem in CF ! I bet that 80% of the users solving this problem either knew this formula from before or found it searching over the internet during the contest and very few actually derived this formula in contest time. That's ridiculous ! Our programming skills should be tested in CF, not our googling skills !!!

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    I thought the problem was really good, and deriving the formula was not that tough(Though I could not get AC in contest time due to a silly mistake :P) but it is disheartening to see so many AC's, courtesy of google. Nevertheless, interesting problem.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I derived it in the contest time also, got WA and sadly it took so much time that I couldn't debug :( And after the contest I noticed that I just forgot to add MOD in a line and in another line an index of an array was mistaken. Other than this, my code was OK and got AC. And there are so many people who knew the trick beforehand and got AC within moments. But again, knowing is a plus point here. I'm just sad that I was so close...

      → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +78 Vote: I do not like it

finally !! i made it in the last moments =)))

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can anyone help me understand why that submission: http://mirror.codeforces.com/contest/932/submission/35308268 takes RTE ? Thank you !

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    What happens if A*i overflows an int?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      Yes, that was the error. Thank you for your time ! I am kind of sad now that I did that stupid mistake

      → Reply
»
7 years ago, # |
  Vote: I like it -7 Vote: I do not like it

i guess the answer for problem E is: sum(n!/(n-i)! * S(k,i) * 2^(n-i) ) with 1<=i<=k and S(k,i) is the stirling number of the second kind if we have k integer(distinct integers) and n sets (with distinct index) so we have C(n,i) ways to choose i sets . Also we have i^k ways to puts k integers into these sets. But also there are always some ways are the same. So I think how to count the repeated ways. For chosen i sets, we have S(k,i) ways to puts k integers into these sets and there are no set without any elements. But the indexs of sets are distinct so we have i! permutations for these sets. For n-i remained sets. We have 2^(n-i) ways to choose the set of these set. This step make the repeated ways to put elements I said before. So the answer is sum(C(n,i)*i!*S(k,i)*2^(n-i) ). with 1<=i<=n. But S(n,k)=0 for any k>n so: result=sum(n!/(n-i)!*S(k,i)*2^(n-i) ) with 1<=i<=k

→ Reply
»
7 years ago, # |
  Vote: I like it +13 Vote: I do not like it

sorry for my bad english. #Lovecommunity

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I have a question. Why I'm not get point on this round?. Firstly I solved 6 problems and get 4th position then my gained point go to zero but why? I didn't understand Enigma27,[user:paran26] , DeshiBasara?

→ Reply
»
3 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Teams was a nice problem, but it's mostly math.

The problem basically wants us to find:

$$$\sum_{i = 1}^N i^K \cdot \binom{N}{i}.$$$

One common trick in dealing with exponentiation is to use the following identity for Stirling Numbers of 2nd Kind:

$$$\sum_{k = 0}^n S(n, k) \binom{x}{k} k! = x^n.$$$

You can prove this using induction if you're not convinced. Anyways, returning to the problem at hand:

$$$\sum_{i = 1}^N i^K \cdot \binom{N}{i} = \sum_{i = 1}^N \binom{N}{i} \sum_{j = 0}^K S(K, j) j! \binom{i}{j} = \sum_{j = 0}^K \sum_{i = 1}^N \frac{N!}{(N - i)!i!} S(K, j) \frac{i!}{j! (i - j)!} \cdot j! = \sum_{j = 0}^K \sum_{i = 1}^N \frac{N!}{(N - i)! (i - j)!} S(K, j).$$$ Now it may seem as if we haven't gotten anywhere because calculating this expression naively is $$$\mathcal{O} (K^2 + NK)$$$ but this is actually pretty useful, mostly because we can play around a bit more. It's equal to:

$$$\sum_{j = 0}^K \sum_{i = 1}^N \frac{(N - j)!}{(N - i)! (i - j)!} \cdot \frac{N!}{(N - j)!} S(K, j) = N!\sum_{j = 0}^K \frac{1}{(N - j)!} \sum_{i = 1}^N \binom{N - j}{N - i}$$$.

Anyways, this gives a final result of: $$$\sum_{j = 0}^k S(K, j) \frac{N!}{(N - j)!} \cdot 2^{N - j}$$$.

This is messier than the first expression, but it is very easy to calculate. We can do the exponentiation using fast binary exponentiation. We can precalculate Stirling numbers in $$$\mathcal{O}(K^2)$$$ using dynamic programming (Stirling numbers have nice recurrence relations). And the rest is easy.

Total complexity is $$$\mathcal{O}(K^2 + \log N)$$$.

NOTE: I remember reading somewhere that Stirling numbers can be computed in better than $$$\mathcal{O}(K^2)$$$ using Lagrange interpolation. However, I can't seem to find where I read that, and I haven't studied interpolation. If this is true, we can make the complexity a little better.

→ Reply