Hi all,
Tomorrow is the first round of OpenCup, Grand Prix of Zheijang. My university got accounts for competitions, and we are planning to take part. I only have one question: Where I can find link for tomorrow round?
Thanks in advance!
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3976 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3482 |
| 8 | hos.lyric | 3382 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3357 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | -is-this-fft- | 165 |
| 3 | Um_nik | 161 |
| 3 | atcoder_official | 161 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 148 |
Hi all,
Tomorrow is the first round of OpenCup, Grand Prix of Zheijang. My university got accounts for competitions, and we are planning to take part. I only have one question: Where I can find link for tomorrow round?
Thanks in advance!
| Name |
|---|



The link will be available on opencup's site shortly before the start
Thank you! I hope we will find it :)
Oh, actually, it is already available.
Yes, I see now. It wasn't available before 30 mintues :)
How to solve any problem?
B:
The string is random, so borders are small (like 50), so you can solve it in length·n, with some suffix array (you can build it naively because the string is random).
Tricky case: all characters the same, when the seed is some solution of linear equation modulo.
Could you elaborate your solution please? I couldn't get the idea to solve it in O(length*n).
G: Theorem in Page 3
Wow, some cool problemsetting from jqdai0815 here.
I solved it with some handwaving like 'let's do some inclusion-exclusion, it's look like determinant, so it must be a determinant.'
This problem is very similar to count the number of tuples of non-intersecting lattice paths. So we can modify the proof of Lindström–Gessel–Viennot lemma to derive this formula.
I am not sure if there is any simple and elementary combinatorial interpretation when you consider this problem in "Young tableaux" way.
I'm not sure that modifying the proof of Lindström–Gessel–Viennot lemma is simple and elementary combinatorial interpretation.
"it's look like determinant", can you explain why it looked like determinant and how exactly you came up withe the formula? I am wondering how the observation/intuition worked to get the formula from scratch
I already solved the problem which used aforementioned Lindström–Gessel–Viennot lemma with the same handwaving.
Funny thing: that problem was solved by 9 teams in the first 1,5 hours, then nobody solved it in 3 next hours, and then I come up with the solution. So I can be almost sure that 9 teams knew that lemma and I 'invented' it on my own.
First, you need to reduce the problem to just counting number of paths from one point to another. It is standard DP in O(m2), so after that we have something like O(n3) left. After I read the problem, I almost right away said 'Oh, there will be some inclusion-exclusion with determinant', because the problem reminded me that lemma. Of course, it was a joke at first :)
Now let's solve n = 2. It looks like brackets sequences, maybe Catalan numbers. How do we get the formula for the Catalan numbers? We count all paths and then subtract bad paths, which we get by using symmetry with respect to diagonal. OK, cool, can we do that for bigger n? Not exactly, it becomes hard. We have to subtract something, but then we subtract something many times and we have to add them back... Oh, maybe there is some inclusion-exclusion?
To make things more convenient I want all inequalities to become strict. It is easy: just add i to i-th coordinate. Why is it more convenient? Because now that symmetry is just swap target values for two coordinates.
Now if I want to do inclusion-exclusion I have to calculate the number of paths without restrictions. It is some multinomial coefficient.
OK, let's start to understand what coefficients should be in our inclusion-exclusion. No swaps — definitely +1. One swap — definitely -1, we should subtract, these are bad paths. Two swaps — not so simple, but looks like +1, we subtract them twice when should have only once. So, what are the objects over which we are taking sum? Permutations of coordinates. And the sign of corresponding element is the parity of number of swaps... yeah, that's the parity of the permutation. So, we are taking sum over all permutations with signs equal to parity of permutation. Doesn't ring a bell?
All that remains is to construct a matrix with right elements. Now we have to recall what are the numbers we want to add together. They are multinomial coefficients. The numerator is constant, and the denominator is a product of some factorials of the form (fpi - si)!, where si is a start for that coordinate and fpi is a finish (the index is different because we mixed them up). In a determinant for a permutation there will be a product of Aipi. Eureka! Just make Aij = ((fj - si)!) - 1.
How did people solve C? Is there a nice solution, or just Karatsuba squeezing?
Let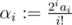 ,
,  ,
, 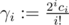 . Then γ is the convolution of α and β. Since each number is of the form "(not very large number) / (odd number)", we can keep it modulo 250 (use modular inverses to divide by odd numbers), and we can use standard FFT. It seems you still need an optimized FFT.
. Then γ is the convolution of α and β. Since each number is of the form "(not very large number) / (odd number)", we can keep it modulo 250 (use modular inverses to divide by odd numbers), and we can use standard FFT. It seems you still need an optimized FFT.
Is F similar to finding shortest paths in expander graph?
Answer in F is a circulation of maximum weight in the given graph, where weights are equals to 1, and capacities are given.
What's the solution for K?
Graph where we are making moves is bipartite. We can have more components(more graphs). In case players are playing in different components — first is the winner if he can make at least one move. If players are in the same component and in the same side of bipartite graph, winner is the first, otherwise if they are from different side winner is the second.
Hmm... what's the justification for this?
Well, we do not have exact proof for all cases. We proved it for first two cases and for case with different side of same bipartite graph we have some intuition.
For first two cases the trick is next: We have starting postion of first player like x and some other position where it can go, for example y. First player all the time can move x - > y - > x - > y - > x... (second player will never block x or y in his moves). So if second player was on some postion p and we have pair (x, p), this pair can repeat again only after even amount of steps for both players (graph is bipartite). So, again first player will come first to position x and second one will lose (maybe I didn't explain well but I hope that point of solution is clear).
For last case when they are from different side of same bipartite graph, in case no cycles in the graph, it can be proven easily that second one is winner(after some amount of moves he can block first player in one node). Case with cycles looks harder to me(we do not have exact proof for that case), but we have shown that player two has winning strategy for cycle of length four, and somehow it was intuitive that for all other cases with even length cycle winner is the same (we checked it with some brute-forces too).
An easier argument for the case where they are from different sides of the bipartite graph: At first, Alice moves to the same side as Bob. Now, it is Bob's turn and they are on the same side. Bob can then just pretend that he's the first player and follow the strategy of Alice from the same side, same component case. Clearly then, Bob wins.
EDIT: this is wrong
aid is rigth, it looks intuitive on first sign :)
At least we didn't spend a lot of time for solving that case :)
This argument is wrong, because in this game history is important. According to you, optimal strategy for Bob is to switch between 2 adjacent vertices, but if Alice also switches between 2 other adjacent vertices, Bob has to move somewhere else.
What's happen is Bob's y=first Alice cell? It looks Bob can switch now between two cells all the time.
It is not possible always, I know.
If Alice hasn't any moves, clearly she loses. So assume, that she has at least one move. From now there 3 main cases.
1) Alice and Bob playing in different components. Then Alice is the winner, she can repeats two connected cells, and the game will looks like that:
Alice can play endless, meanwhile Bob has to choose new cells every time, so he loses.
2) Alice and Bob playing in the same component and they are starting on the same colored cells(bipartite coloring). Then Alice again wins. She could repeat the same strategy. The proof is kind of easy: let's assume Alice repeat the same strategy, but Bob is winning. As we can see above, the only possibility for Alice not to move from
a0toa1is the Bob ina1, but this couldn't happen, because they can be on different colored cells only after Alice's move, contradiction.3) Alice and Bob playing in the same component and they are starting on the different colored cells(bipartite coloring). Assume, that Alice made her first move to
a1.Then the strategy for Bob can be the following: just move to Alice, until one of two things happened:a0nora1a0ora1see below
I'm not sure if I understand your strategy for 'the first thing' of case three correctly. Do you propose that Bob from that point on switches between two cells indefinitely? In that case it seems wrong to me.
My proof for the third case: Bob chooses a path towards Alice. He starts switching between the first two cells of that path until Alice revisits her starting square. Then Bob starts switching between the next two cells from the path until Alice revisits her starting square for the second time. This process continues until one of the two squares Bob is switching between is equal to Alice's starting cell, in which case it is impossible for Alice to return to her starting cell and she must eventually run out of moves, so Bob wins.
Is problem F somewhat known? Even after coming up with right reduction we didn't come up with any fast solution. Then we looked in authors code, our MCMF with dijkstra gets TL, and our MCMF with FB on queue works in 1.99s, but I don't see any problems with getting AC on OpenCup.
And for problem C: does all the teams know how to write FFT modulo 2k or they just copy-pasted it? Or did something else? I didn't even know about such algorithm before.
Is it something special (not square root idea for general modulo)? Can you describe the idea in few words? I mean 2^k FFT.
Fast convolution for 64-bit integers
Nice, thanks
Actually, I don't even know if MCMF with FB on the queue is a polynomial solution.
For problem C, my solution just divides each integer into 3 pieces, like the trick used to module 10^9+7. I didn't know FFT module 2^k algorithm when I prepared this problem.
It's the author's solution, isn't it? We looked in the code (well, not exactly we but Burunduk1) and there is only some MCMF with something on queue.
Did you guys really read the main correct solution?
And I don't want to fail your solution intentionally. I forgot to enlarge the time limit after testing this solution :(
OK, so if we didn't, can you please tell us your solution?
For F: did your MCMF have negative cycles? You have to find cycles of min average weight with FB if you want this to be polynomial at all.
There is a standard MCMF algorithm with cost scaling and push-relabel inside (edit: e.g.), it is challenging to implement it from scratch, but prewritten code is allowed, so...
I didn't know F beforehand, but I was pretty confident that my MCMF with push-relabel cost scaling would pass. My flow graph contains only m edges and n + 2 vertices. (It passed in 0.773s (or 0.829 if you model as min cost circulation with weights - 1 instead), MCMF code is on github. The code is fast and works with negative cycles.).
Regarding C: I always use FFT (and not NTT), so I don't have to care about special modulos and the only possible issue is the size of the coefficients. There's a know trick of splitting the coefficient into lower and higher bits to handle larger numbers. My prewritten code (function poly_mul_split on github) already does this once to handle coefficients up to 109 with only 3 calls to FFT per polynomial multiplication. One trick used there is to use both the real and imaginary part to run 2 FFTs in parallel.
To handle coefficients up to 250, split into 25 bits each and do a Karazuba step on the coefficients (compute convolutions using only high bits, only low bits and sum of low and high bits, subtract the sum of first two from the third, then add the results coefficient wise shifted by 50, 0 and 25.). This results in 3 calls to 109-coefficient-polynomial multiplication, so 9 calls to FFT in total. My code runs in 0.666s, so there's quite a bit of leeway.
OK, this is lame. I'm happy for you and your super-fast library.
Huh? You can solve this problem in 6 FFT in total. code
0.752s, though
Huch! You can solve it with only 5 calls to FFT. code.
338ms
Somehow I lacked some precision when trying to split in 3 parts instead of 4... :(
Well, this time it really seems pretty tight though
Problem I showcases how cruel we've got in only 18 years..
I think I solved line in (just combination of some techniques), but not sure when it's a cycle. Any ideas?
(just combination of some techniques), but not sure when it's a cycle. Any ideas?
Technique in 2012 (wqs/clj binary search / tricks from aliens) + Technique in 2010 (http://mirror.codeforces.com/gym/100020/problem/I)
BTW, how to solve the line case in ? I can only solve it in
? I can only solve it in 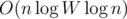 or
or 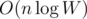 (using SMAWK algorithm).
(using SMAWK algorithm).
I tried to say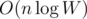 :) Cost function is Monge, so I thought this trick will work.
:) Cost function is Monge, so I thought this trick will work.
Any ideas for D?
Btw, this is probably the most challenging problemset I have ever encountered, it feels so good :)
Does anybody know how to solve J? If we could calculate the number of ways to go from (0, 0) to (x, x) for all x with ignoring falling in holes, we can solve whole problem by some kind of online-FFT technique, but I don't have any idea to do such a thing...
The probability is P-recursive. You can read the blog of min-25 for his excellent code. And you can read the chapter 6 of enumerative combinatorial for the theory about the P-recursive sequence.
Tnak you.
The set is very nice. Many problems are around some new technique. May be some hints for the remaining problems?
A, D, E, H, L
L:
Actually this problem is discussed in the paper. But my solution is not related to this paper.
You can think the problem in this way. We want to know the time when it gets contracted for each edge.
So we can solve this problem offline by a divide and conquer algorithm solve(l,r,E), which means we only know all the edges in the set E are contracted in time [l,r].
Let m=(l+r)/2, we added all the edges in E appeared before time m, and run the Tarjan algorithm on these edges, the time complexity for this part is O(|E|). E are divided into two sets E1, E2 depends on whether the edge gets contracted in time m. Then we can solve(l,m,E1) and solve(m+1,r,E2).
For each edge, it will only appear once in each level. The time complexity is O(E log E).
A:
Let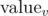 be the product of factorials of sizes of groups of isomorphic children. For example, if v has 7 children {u0}, {u1, u2}, {u3, u4, u5, u6}, then
be the product of factorials of sizes of groups of isomorphic children. For example, if v has 7 children {u0}, {u1, u2}, {u3, u4, u5, u6}, then 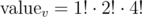 . The answer for the subtree rooted in x is the product of all
. The answer for the subtree rooted in x is the product of all 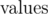 in it's subtree.
in it's subtree.
Define hash of the rooted tree in the following way: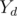 if root has no children and
if root has no children and 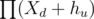 over all children otherwise. d is the distance to the global root, {X} and {Y} are some random numbers.
over all children otherwise. d is the distance to the global root, {X} and {Y} are some random numbers.
Let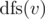 return the following structure: key is some node x in the subtree of v, value is the hash of subtree rooted at v at the time when x was added. Now at node v we can simulate process of adding vertices, but with one exception: ignore vertices from the biggest child if it is already bigger than the second biggest child. It is enough to generate all needed events. For merging structures from children we will need to be able to apply some linear functions to subsegment of keys in structure, insert item in some position, merge 2 structures. Treap is sufficient here.
return the following structure: key is some node x in the subtree of v, value is the hash of subtree rooted at v at the time when x was added. Now at node v we can simulate process of adding vertices, but with one exception: ignore vertices from the biggest child if it is already bigger than the second biggest child. It is enough to generate all needed events. For merging structures from children we will need to be able to apply some linear functions to subsegment of keys in structure, insert item in some position, merge 2 structures. Treap is sufficient here.
The final complexity is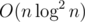 .
.
H:
Lets keep a set of directed paths where the following condition holds for each node of the path except the last: the node directly after this node in the permutation (if any) can only be an earlier node or the next node of the path. Initially each node is its own path. Now we search for the head of any path which has exactly one outgoing edge to another path. If this happens to be tail of the other path we can concatenate both paths and repeat. Otherwise we have special case 1 which we handle separately (see remarks at the end).
If after the process above finishes we have more than one path, there is no solution (we can never leave the path in which we start). Otherwise we have found one solution (just follow the path), but there may be more. When there is no edge from the head to the tail (which turns the path into a cycle) we have special case 2 which we also handle separately (see remarks at the end). Otherwise we can start in any node of the path, provided there is no 'back edge' (other than the cycle-closing edge) that 'covers' us, which is easy to check with a prefix-sum-like datastructure.
There are two special cases left that need to be handled. For special case 1 we know that the last nodes of the permutation must be either the path that points to the middle of another path or the nodes of the other path before the node that is being pointed at. We can just try both cases with minor modifications of the algorithm above (only extend paths outside the final vertex set, append the final vertexes at the head of the path afterwards, and there will never be more than one solution). For special case 2 an other solution is only possible if there is at least one edge to the tail of the path. In this case the last nodes of the permutation must be the prefix of the path upto the last node that has such an edge and we can handle this in the same way as special case 1.
The above can be implemented in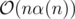 . I enjoyed solving this problem, too bad I couldn't make it work during the contest (mostly because I was overcomplicating it), but I have it accepted afterwards. I have omitted most of the proofs, but when drawing some cases on paper they should be rather obvious.
. I enjoyed solving this problem, too bad I couldn't make it work during the contest (mostly because I was overcomplicating it), but I have it accepted afterwards. I have omitted most of the proofs, but when drawing some cases on paper they should be rather obvious.
This one is my favorite problem in the problem set. Thank you for sharing your solutions.