Facebook Hacker Cup 2014: Round 2

→ Обратите внимание

До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
09:05:12
Зарегистрироваться »

*есть доп. регистрация

→ Трансляции

Leetcode BiWeekly Contest 144 — Solution Discussion

Shayan

До начала 10:35:12

Codeforces CodeTON Round 9 (Div 1 + Div 2) — Solution Discussion

Shayan

До начала 12:05:12

Всё →

→ Лидеры (рейтинг)

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

Страны | Города | Организации

Всё →

→ Лидеры (вклад)

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
4	atcoder_official	161
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Всё →

→ Найти пользователя

→ Прямой эфир

Детальнее →

Блог пользователя eduardische

Facebook Hacker Cup 2014: Round 2

Автор eduardische, 11 лет назад, По-русски

И пока все отходят от ТопКодера, напоминаю, что 15го в 1:00 по Москве пройдёт второй раунд Facebook Hacker Cup 2014. Продлится он 3 часа. Топ 100 проходят дальше и получают майки.

facebook, hacker cup, 2014, второй раунд, майки

eduardische
11 лет назад
23

Комментарии (23)

Написать комментарий?

eduardische

11 лет назад, # |

The contest will be available here.

→ Ответить

geek_guy

11 лет назад, # |

← Rev. 2 →

All those who could not qualify for this round (like me)can view leader board here !

→ Ответить

yarrr

11 лет назад, # |

+19

Стандартный вопрос: А как решать 35 и 40?

→ Ответить

marat.snowbear

11 лет назад, # ^ |

Плюсую за 35. Сам заслал Монте-Карло на последних минутах от безысходности.

→ Ответить

yarrr

11 лет назад, # ^ |

Я тоже, не заходит, я потом от безысходности почекал.

→ Ответить

yeputons

11 лет назад, # ^ |

← Rev. 2 →

В 35 я взял и расписал всё нафиг. Но это такой отстой...

Будем считать количество раскладов, при которых мы выиграем.
Зафиксировали минимальные карты у трёх игроков
Теперь их максимальные карты лежат в каких-то отрезках
И эти отрезки друг в друга вложены в нужном порядке.
Теперь добавили какую-то цэшку, чтобы выбрать несколько разных элементов из трёх вложенных отрезков.

Оптимизация с куба до квадрата на запрос:

Самый вложенный цикл у меня зависит только от a₃ и какой-то внешней константы (если разделить на два слагаемых, а одно домножить потом). Предподсчитаем эти два слагаемых.
Получили квадрат плюс квадрат на запрос.

→ Ответить

Egor

11 лет назад, # ^ |

+16

У меня линия на запрос. Следующая динамика:

Пусть small — наша меньшая карта, big — большая. Тогда в любой момент времени перебираем младшую карту остальных пар сверху вниз. Кроме этого мы в динамике знаем сколько еще пар осталось и в скольких уже посчитанных парах меньшая карта больше, чем small. Из динамики 2 перехода — либо мы не берем текущую карту в качестве младшей (и тогда тупо уменьшаем это значение), либо мы ее берем. Тогда у нас есть ограничение сверху на эту карту (мы точно знаем, что мы победили) и снизу (она должна быть старше младшей карты в своей паре, а еще старше small, если во всех оставшихся парах все карты младше, чем small — это отдельно считается цешечкой). Кроме того мы знаем сколько карт уже использовано с этого отрезка — можно посчитать число вариантов

→ Ответить

caustique

11 лет назад, # ^ |

Ну 35 я попробовал решить так.

Посчитаем величины cnt[i][j][k] = сколько пар (x, y), таких что x+y=i, существует, причем никакое из чисел x и y не равно никакому из чисел j и k.

Тогда посчитаем величины bad и total — плохие для нас расклады и общее количество. Просто просуммируем все значения cnt[sum][c1][c2], где sum>c1+c2, а случай, когда выигрывают по наибольшей карте, разберем циклом фор отдельно.

Ну а дальше обычная магия — умножим bad на 3, потому что 3 игрока против нас играют, значит вероятность проиграть в 3 раза больше.

Это дает нам на третий сэмпл вероятность проигрыша 0.6, а значит вероятность выигрыша 0.4.

Ну в итоге формула выходит: if (3 * total — 12 * bad > 0) then "B" else "F"

→ Ответить

Sereja

11 лет назад, # ^ |

-13

35 я делал немного необычно. Для одной пары можно написать ДП(i, i1, i2, i3) — какую карту смотрим, какие уже у соперников, ну или 0 если еще нету или 101, если уже у них пара. Динамика хранит сколько комбинаций таких, что выиграем мы.

Возьмем и бин поиском найдем самую галимую пару, которая несет профит. Забьем константу. Теперь просто сверим пару на входе и найденную ранее. Так для каждого Н.

→ Ответить

Petr

11 лет назад, # ^ |

Ну 40 довольно тупая. Заметим, что в вершину i можно добавлять ребра только из таких вершины j, что j<i и a[a[a[...a[j]...]]]=a[i]. Значит есть 2^(количество таких)-1 вариантов — но нужно ведь ещё, чтобы не было такой вершины ближе, значит нужно вычесть 2^(количество таких j<i, что a[a[a[...]]]=k)-1 для каждого k<i, что a[k]=a[i] — это мы перебираем ту, которая будет ближе.

→ Ответить

ilyakor

11 лет назад, # ^ |

← Rev. 2 →

40 — нам дают дерево, надо посчитать количество способов сделать новый граф весьма странным образом. Если подумать, разрешается добавлять рёбра в из вершины в поддерево её предка в дереве, но при этом не должно оказаться, что все эти рёбра только в одном поддереве какого-то из детей предка. Т.е. если обозначить c_x количество вершин в поддереве вершины x, ответ умножается на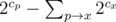 $\text{[math]}$ (ну, +-1, не забываем про пустое множество), ну или как-то так.

35 — фиг знает как честно решать, я засабмитил лажу за n⁵, написанную на плюсах; как ни странно, довольно быстро работала. Т.е. я для каждого запроса просто перебрал одного из оппонентов, а для оставшихся 2х посчитал всё за линейный проход включениями-исключениями.

→ Ответить

AlexSkidanov

11 лет назад, # ^ |

40 там несколько решений. Одно из решений -- вершину a, для которой все пути должны идти через b, надо либо подцепить непосредственно к b, либо к двум вершинам из двух разных поддеревьев b. После этого ее можно дополнительно соединить с любым множеством вершин из поддерева с корнем в b. Это делается динамикой. Я сам решал немного иначе, но у меня int вместо long long, так что там все понятно :о)

→ Ответить

eduardische

11 лет назад, # ^ |

← Rev. 4 →

Моё решение по 35. В качестве главной морали позволю процитировать yeputons : "В 35 я взял и расписал всё нафиг. Но это такой отстой..."

Зафиксируем N, X, Y и одного противника. Пускай его карты A < B. У нас есть 6 вариантов:

           X    Y
   lose AB
   lose  A   B
depends  A        B
depends      AB
    win      A    B
    win           AB

Нас интересуют только первые 4. Соответственно при данном N, X, Y перебираем все 64 варианта по типу руки у соперника. Нам надо чтобы все три соперника нам проиграли 3й и 4й делаем ДП преподсчётом (при этом в ДП добавляем измерение количества взятых пар), чтобы оставить только проигрышные варианты. 3е ДП простое, 4е ДП посложнее. Вспомогательная картинка (если перебираем по позициям B — то прямоугольники это доступные позиции для А). Теперь можно для фиксированного N, X, Y в обоих случаях сделать ДП a[cnt][last] — количество вариантов выбрать cnt пар, проигрывающих нам, при этом последний невыбранный B — last. В случае второй половины варианта 4, и вариантов 1 & 2; нам известно количество свободных карт в каждой группе, и мы можем необходимое домножить на C-шки, так как нам годится любая комбинация из них, и там можно просто аккуратно (ключевое слово всей задачи) домножить всё. Ну и получаем кол-во выйгрышных раскладов и проверяем является ли эта величина умноженная на 4 больше общего числа вариантов. Асимптотика: O(P * N^5 + T * Q * 4^P), где P — количество игроков. На всякий, код.

→ Ответить

eatmore

11 лет назад, # ^ |

+16

Расскажу своё решение 35, оно разбирает один случай за O(n) и даёт точный ответ (число выигрышных комбинаций).

Используется формула включения-исключения: берётся куб числа способов выбрать вторую пару и из него аккуратно вычитаются те комбинации, в которых пары перекрываются. Вначале для каждого i посчитаем число таких j ≤ i, что j ≠ c1, c2. Теперь число способов выбрать две перекрывающиеся пары считается легко: перебираем общий элемент, для каждого значения прибавляем квадрат числа способов дополнить этот элемент до пары. Те комбинации, где перекрываются оба элемента, будут учтены по два раза, придётся скорректировать. Остались случаи, когда перекрываются все три пары. Здесь есть три варианта: "пропеллер", "треугольник" и "цепочка". Третий вариант — самый сложный, расскажу, как делать его. Считается вспомогательная динамика: для каждого i число таких j, что i ≠ j и пара (i, j) нас не обыгрывает. По этой динамике считаются частичные суммы. Теперь перебираем один из средних элементов цепочки. Число способов выбрать один крайний элемент — первая динамика, число способов выбрать оставшиеся два элемента — вторая динамика. В результат будут (ошибочно) входить цепочки, в которых некоторые (не соседние) элементы совпадают, но это либо "треугольники", либо более короткие цепочки — таким образом, всё, что нужно, чтобы отсеять эти варианты, уже посчитано. Осталось правильно подобрать коэффициенты.

Поскольку все динамики полиномиальные (а не экспоненциальные, в смысле значений), а условия достаточно простые, я сильно подозреваю, что для этой задачи можно найти явную формулу (или несколько, в зависимости от условий вида c1 + c2 < n).

→ Ответить

iensen

11 лет назад, # |

← Rev. 2 →

Кто-нибудь может по-русски объяснить, что имелось ввиду под "path" в 40?

→ Ответить

eduardische

11 лет назад, # |

← Rev. 2 →

Интересно, орги ошиблись в оценке задач, или самплы в 40 настолько слабые, что у многих будет падать? Потому что пока сабмитов по 40 явно больше чем по 35.

UPD: Йес, моё 20 + 35 таки зашло в топ 100. Таки много упало, видимо.

→ Ответить

Sereja

11 лет назад, # ^ |

Я хотел писать не одно решение, но находил контр-примеры. Думаю, немало упадет.

→ Ответить

Xellos

11 лет назад, # |

← Rev. 2 →

-10

My thoughts about the problems:

WAT? 3 times combinatorics? It's too narrow, even if all 3 problems could be solved in different ways...

Hm, the results are out. WAT? again, I flew up 100 places and got to round 3... submitting 5 minutes before the end, like a boss :D

Problem 1 was suitably easy, just two pointers using set<>s to store the sets of colours was sufficient.

Problem 3 was also suitably hard, requiring the right idea, and an efficient, although not difficult, implementation.

I managed to finalize this idea about 30 minutes before the end: Every vertex i gives us the number of ways P_i to choose slopes leading to it directly, and it's only dependent on the first i numbers of the input (denote those as A_i). To find it, we construct a tree where vertex j is the son of vertex A_j. If we add a direct slope from j < i to i, every path containing that slope will be passing through every vertex on the path from the root (vertex 0) to j, and there will be some path not passing through any vertex not on that path and < i, so A_i must be on that path, or equivalently, we can only add direct slopes to i from children of A_i in that tree. By the same idea, we find out that those direct slopes can't all be from the subtree of one of the sons of A_i; if those sons have subtree sizes S_1..k, then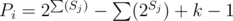 $\text{[math]}$ . All that's left is constructing the tree, counting 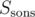$\text{[math]}$ by one DFS and counting P_i, all in O(N), giving us O(N²) total complexity. I wonder if it could be solved more efficiently...

I didn't like problem 2, though. I couldn't escape a lot of casework by inclusion/exclusion... is there any nice way to solve it?

→ Ответить

Alex_2oo8

11 лет назад, # ^ |

← Rev. 3 →

+24

Problem 3 is solvable in O(N log² N) time (UPD: WRONG). All that we need is to keep track of sizes of subtrees. Let build an heavy light decomposition on the whole tree (with all N vertices). Then after processing vertex i, we will add it to the tree. Adding vertex is equivalent to increasing by one all sizes on the path from the root to this vertex.

Of course, for this problem it is an overkill and during the competition I've implemented O(N²) one :)

→ Ответить

rng_58

11 лет назад, # ^ |

+24

In the worst case you need to get sizes of subtrees O(N²) times (for example when A_i = 0 for all i).

O(N⁵) brute force worked in Problem 2...

→ Ответить

Alex_2oo8

11 лет назад, # ^ |

← Rev. 2 →

Ok, you are right. But, if I'm not wrong again (at least now is not 3 AM), there is an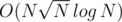 $\text{[math]}$ solution.

Let construct the whole tree and divide there all vertices into two sets: big and small vertices. Big vertices will be all vertices with size of subtree (in the whole tree) greater than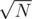 $\text{[math]}$ , small will be all other vertices. Also, like in the first (slow) solution, let build an heavy light decomposition on the whole tree.

Now, we will again add to the tree vertices one by one, but we will keep track of two values:

S_V — size of subtree in current tree and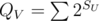 $\text{[math]}$ , where U is looping through all small sons of vertex V.

Now, how we will add a vertex: I can't explain it clearly in words, so the pseudocode:

add(v) {
  while (v is small vertex) {
    S[v] += 1;
    Q[ parent[v] ] += pow(2, S[v]) - pow(2, S[v] - 1);

    v = parent[v];
  }
// Now all vertices on path from root to v are big,
// so they won't counts in any Q[x]

  update all sizes on path from root to v;
// this part takes O(log^2 N) using HLD
}

I hope it's clear, that while loop will iterate at most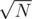 $\text{[math]}$ times per vertex, so adding one vertex takes 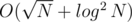$\text{[math]}$ time.

Now, how to calculate P_V (from Xellos comment):

$\text{[math]}$ , where U is looping through all big sons of vertex V. This step takes $\text{[math]}$ time, because each vertex has at most $\text{[math]}$ big sons.

So, the overall complexity of this solution is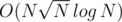 $\text{[math]}$ .

→ Ответить

thocevar

11 лет назад, # ^ |

+29

You can solve Problem 2 with dynamic programming in O(n). You can count the remaining three pairs from those with higher maximum numbers towards lower. Let's say that pair (x, y), x < y will be the largest. If you fix y, you can choose x from somewhere in the range 1..x'. When you'll have to choose the next pair (a, b), b<y, you know that the range of possible values for a will be 1..a', x' ≤ a'. Therefore, it doesn't matter which x was chosen in the previous step, only how many pairs were chosen before.

In fact you're solving a generalized problem f(k, n) of choosing k pairs from numbers 1..n such that their sum is at most c₁ + c₂. Time complexity is just O(kn). You either use n as a part of the largest pair or not. There are a couple of things to consider, like how to handle used values c₁, c₂ and make sure that x < y, but it can be done.

→ Ответить

sbasrik

11 лет назад, # ^ |

← Rev. 2 →

Pretty nice approach,thanks for sharing

→ Ответить

Соревнования по программированию 2.0

Время на сервере: 23.11.2024 08:29:48 (l2).

Десктопная версия, переключиться на мобильную.

При поддержке