544A - Set of Strings
In that task you need to implement what was written in the statements. Let's iterate over all characters of string and keep array used. Also let's keep current string. If current character was not used previously, then let's put current string to the answer and after that we need to clear current string. Otherwise, let's append current character to the current string. If array, that contain answer will have more then k elements, we will concatenate few last strings.
The jury solution: 11035685
544B - Sea and Islands
It's clear to understand, that optimal answer will consists of simple cells, for which following condition fullfills: the sum of indices of row and column is even. We will try to put k islands in such way, and if it's impossible, we will report that answer is NO. Try to prove that this solution is optimal.
The jury solution: 11035691
543A - Writing Code
Let's create the solution, which will work too slow, but after that we will improve it. Let's calculate the following dynamic programming z[i][j][k] — answer to the problem, if we already used exactly i programmers, writed exactly j lines of code, and there are exactly k bugs. How we can do transitions in such dp? We can suppose that we i-th programmer will write r lines of code, then we should add to z[i][j][k] value z[i - 1][j - r][k - ra[i]]
But let's look at transitions from the other side. It's clear, that there are exactly 2 cases. The first case, we will give any task for i-th programmer. So, we should add to z[i][j][k] value z[i - 1][j][k]. The second case, is to give at least one task to i-th programmer. So, this value will be included in that state: z[i][j - 1][k - a[i]]. In that solution we use same idea, which is used to calculate binomial coefficients using Pascal's triangle. So overall solution will have complexity: O(n3)
The jury solution: 11035704
543B - Destroying Roads
Let's solve easiest task. We have only one pair of vertices, and we need to calculate smallest amout of edges, such that there is a path from first of vertex to the second. It's clear, that the answer for that problem equals to shortest distance from first vertex to the second.
Let's come back to initial task. Let's d[i][j] — shortest distance between i and j. You can calculate such matrix using bfs from each vertex.
Now we need to handle two cases:
- Paths doesn't intersects. In such way we can update the answer with the following value: m - d[s0][t0] - d[s1][t1] (just in case wheh conditions on the paths lengths fullfills).
- Otherwise paths are intersecting, and the correct answer looks like a letter 'H'. More formally, at the start two paths will consists wiht different edges, after that paths will consists with same edges, and will finish with different edges. Let's iterate over pairs (i, j) — the start and the finish vertices of the same part of paths. Then we can update answer with the following value: m - d[s0][i] - d[i][j] - d[j][t0] - d[s1][i] - d[j][t1] (just in case wheh conditions on the paths lengths fullfills).
Please note, that we need to swap vertices s0 and t0, and recheck the second case, because in some situations it's better to connect vertex t0 with vertex i and s0 with vertex j. Solutions, which didn't handle that case failed system test on testcase 11.
The jury solution: 11035716
543C - Remembering Strings
First that we need to notice, that is amout of strings is smaller then alphabet size. It means, that we can always change some character to another, because at least one character is not used by some string.
After that we need handle two cases:
- We can change exactly one character to another. The cost of such operation equals to a[i][j] (which depends on chosed column) After that we can remember string very easy.
- We can choose some column, and choose some set of strings, that have same character in that column, By one move we can make all these strings are easy to remember.The cost of such move equals to cost of all characters, except most expensive.
As the result, we will have following solution: d[mask] — answer to the problem, when we make all strings from set mask easy to remember. We can calculate this dp in following way: let lowbit — smallest element of set mask. It's clear, that we can do this string easy to remember using first or second move. So we need just iterate over possible columns, and try first or second move (in second move we should choose set that contain string lowbit) Overall complexity is O(m2n), where m — is length of strings.
The jury solution: 11035719
543D - Road Improvement
Let's suppose i is a root of tree. Let's calculate extra dynamic programming d[i] — answer to the problem for sub-tree with root i We can understand, that d[i] equals to the following value: 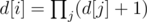 — where j is a child of the vertex i. It's nice. After that answer to problem for first vertex equal to d[1].
— where j is a child of the vertex i. It's nice. After that answer to problem for first vertex equal to d[1].
After that let's study how to make child j of current root i as new root of tree. We need to recalculate only two values d[i] and d[j]. First value we can recalculate using following formula d[i]: suf[i][j] * pref[i][j] * d[parent], where parent — is the parent of vertex i, (for vertex 1 d[parent] = 1), and array suf[i][j] — is the product of values d[k], for all childs of vertex i and k < j (pref[i][j] have same definition, but k > j). And after we can calculate d[j] as d[j] * (d[i] + 1). That is all, j is root now, and answer to vertex j equals to current value d[j]
The jury solution: 11035737
543E - Listening to Music
Let's sort all songs in decreasing order. We will iterate over songs, and each time we will say, that now current song will fully satisfy our conditions. So, let's si = 0, is song i was not processed yet and si = 1 otherwise. Let 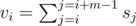 . It's clear, when we add new song in position idx then we should do + 1 for all on segment [max(0, idx - m + 1), idx] in our array v. So, when we need to implement some data structure, which can restore our array v to the position when all strings have quality ≥ q. It also should use very small amout of memory. So, answer to the query will be m - max(vi), lj ≤ i ≤ rj.
. It's clear, when we add new song in position idx then we should do + 1 for all on segment [max(0, idx - m + 1), idx] in our array v. So, when we need to implement some data structure, which can restore our array v to the position when all strings have quality ≥ q. It also should use very small amout of memory. So, answer to the query will be m - max(vi), lj ≤ i ≤ rj.
We will store this data structure in the following way. Let's beat all positions of songs in blocks of length  . Each time, when we added about
. Each time, when we added about  songs as good, we will store three arrays: first array will contain value vi of first element of the block of indices. second array will contain maximum value of v on each block and also we will keep about
songs as good, we will store three arrays: first array will contain value vi of first element of the block of indices. second array will contain maximum value of v on each block and also we will keep about 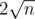 of ''small'' updates which doesn't cover full block. Using this information array v will be restored and we process current query in easy way.
of ''small'' updates which doesn't cover full block. Using this information array v will be restored and we process current query in easy way.
The jury solution: 11035739









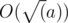 to calculate the beauty. Also you can make your solution more faster, it you will precalculate some small primes. Also you can use
to calculate the beauty. Also you can make your solution more faster, it you will precalculate some small primes. Also you can use 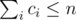 . After that let's calculate the following DP:
. After that let's calculate the following DP: 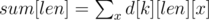 , where
, where 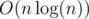 of memory, also you can build it in
of memory, also you can build it in  time /
time / 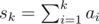 ;
;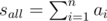 ;
;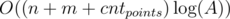 .
.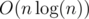
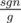 , where
, where 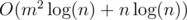 .
.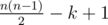 .
. . For other circles it's quite simple to calculate sum of distances. There are
. For other circles it's quite simple to calculate sum of distances. There are 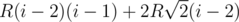 . In the same manner we can calculate answer for cirlcles which are located to the right of the current circle
. In the same manner we can calculate answer for cirlcles which are located to the right of the current circle
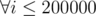 ,
, 


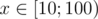 divisible by 10 we take it.
divisible by 10 we take it. and then check equality of corresponding
and then check equality of corresponding 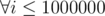 . Let
. Let 
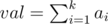 .
. 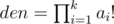 , you can easily prove it using facts about prime powers in factorial and following inequality
, you can easily prove it using facts about prime powers in factorial and following inequality 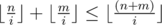 . By the way,
. By the way, 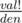 is called multinomial coefficient. So answer can't exceed
is called multinomial coefficient. So answer can't exceed 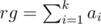 .
.
