544A - Набор строк
В этой задаче нужно написать то, что написано в условии. Для этого можно воспользоваться массивом, с помощью которого мы будем понимать встречалась буква до этого. Будем будем обрабатывать символы по очереди. И поддерживать некоторую строчку. Если текущий символ ещё не встречался, то тогда начнём новую строку, а текущую строку мы положим в массив ответа. Иначе добавим текущий символ конец текущей строки.
Если в массиве ответа окажется больше чем к строк, то тогда сконкатенируем на несколько последних в одну.
Авторское решение: 11035685
544B - Море и острова
В эти задачи нетрудно понять что оптимальный ответ всегда состоит из одиночных клеток обладающих следущим свойством: сумма индекса строчки и столбца четная. Таким образом попробуем разместить ровно k островков в этих в клетках, если не получится, то ответ на задачу NO. Попробуйте доказать почему всегда так действовать оптимально.
Авторское решение: 11035691
543A - Пишем код
Давайте для начала придумаем решение который будет работать медленнее чем нужно. Будем решать задачи динамическим программированием: z[i][j][k] — мы обработали ровно i программистов, написали ровно j строчек кода и при этом возникло ровно k ошибок. Как сделать в такой динамике переходы? Очень просто, переберём сколько строчек напишет i программист (пусть r) и прибавим к z[i][j][k] значение z[i][j - r][k - r[ai]]. Однако давайте посмотрим на переходы с другой стороны. Очевидно, что i программист либо не напишет ни одной строчки, тогда к ответу прибавится значение z[i - 1][j][k], либо он напишет одну строчку, а остальные строчки учтутся в значении z[i][j - 1][k - a[i]]. Здесь можно провести аналогию c подсчетом биномиальных коэффициентов c помощью треугольника паскаля. Таким образом получим решение за ассимптотику O(n3)
Авторское решение: 11035704
543B - Разрушение дорог
Для начала попробуем решить задачу проще: задана пара вершин, нужно определить минимальный набор ребер, который нужно оставить, чтобы существовал путь из одной вершины, в другую. Очевидно, это число в точности равно кратчайшему расстоянию между вершинами.
Теперь перейдем к искомой задаче. Пусть d[i][j] — кратчайшее расстояние между вершинами. Такую матрицу очень просто насчитать, запустив из каждой из n вершин bfs. Отлично
Теперь разберем два случая: Пути не пересекаются, тогда ответ можно обновить числом m - d[s1][t1] - d[s2][t2] (при условии, что выполнены условия на длину путей). Иначе, заметим что если пути пересекаются, то тогда тогда ответ имеет вид буквы Н. Более формально, сначала каждый из путей будет содержать различные ребра, потом несколько общих ребер, идущих подряд, и затем каждый из путей будет содержать различные ребра. Таким образом, переберем первую и последнюю общие вершины пути. Пусть эти величины равны (i, j). Тогда обновим ответ величиной m - d[s1][i] - d[i][j] - d[j][t1] - d[s2][i] - d[j][t2] (при условии, что выполняются ограничения на длину путей). Стоит отметить, что также стоит обменять вершины s1 и t1 местами, и снова обновить ответ, поскольку иногда выгодно соединить t1 и с вершиной i, а s1 с вершиной j. Решения, которые не учитывали это не проходили 11 тест
Авторское решение: 11035716
543C - Запоминаем строки
Во первых стоит отметить важный факт: количество строк меньше длины алфавита. Таким образом, всегда когда мы хотим сделать замену символа на другой, мы всегда сможем найти подходящий другой символ.
Далее возможны две ситуации: за одну операцию мы можем взять и заменить символ на любой другой, за это мы заплатим a[i][j] денег ( в зависимости от столбца, в котором мы сделаем строку уникальной). Либо за мы можем взять некоторый столбец, и рассмотреть некоторое множество строк, имеющих одинаковый символ в заданном столбце, и все сделать их уникальными. За это мы оплатим стоимость замены всех символов, кроме одного: самого дорого. Таким образом, получим решение: d[mask] — ответ на задачу, если мы сделали все строки, отвечающие за единичные биты уникальными. Как пересчитывать такую динамику? Пусть lowbit — младший единичный бит. Тогда очевидно, что мы сделаем его уникальным либо с помощью первой операции, либо с помощью второй. Для этого, переберем столбец и рассмотрим множество строк, имеющих такой же символ с со строкой lowbit. И обновим ответ соответствующим значением. Получим решение за ассимптотику O(m2n), где m — длина строки.
Авторское решение: 11035719
543D - Улучшение дорог
Подвесим дерево за вершину 1. Для начала подсчитаем вспомогательную динамику d[i] — количество способов починить дороги для поддерева с корнем в вершине i. Как такую динамику пересчитывать 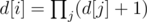 — где j это дети вершины i. Отлично. Таким образом ответ на задачу для вершины 1 — это d[1] Далее научимся переподвешивать дерево за некоторого ребенка j текущей вершины i. Очевидно, пересчитаем величину d[i]: suf[i][j] * pref[i][j] * d[parent], где parent — это родитель вершины i, (для вершины 1 d[parent] = 1), а массивы suf[i][j] — это произведение величин d[k], для всех детей i, k < j (pref[i][j] — k > j). После этого, обновим значение d[j] значением d[j] * (d[i] + 1). Все, теперь вершина j стала корнем, и ответ для нее — текущее значение d[j]
— где j это дети вершины i. Отлично. Таким образом ответ на задачу для вершины 1 — это d[1] Далее научимся переподвешивать дерево за некоторого ребенка j текущей вершины i. Очевидно, пересчитаем величину d[i]: suf[i][j] * pref[i][j] * d[parent], где parent — это родитель вершины i, (для вершины 1 d[parent] = 1), а массивы suf[i][j] — это произведение величин d[k], для всех детей i, k < j (pref[i][j] — k > j). После этого, обновим значение d[j] значением d[j] * (d[i] + 1). Все, теперь вершина j стала корнем, и ответ для нее — текущее значение d[j]
Авторское решение: 11035737
543E - Слушаем музыку
Отсортируем песни по убыванию. Будем последовательно рассматривать песни и говорить, что теперь песня хорошая и удовлетворяет критерию качества. Пусть si = 0, если песня с номером i еще не добавлена в рассмотрение, и si = 1 иначе. Тогда пусть 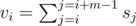 . Очевидно, когда мы добавляем новую песню позиции idx в рассмотрение, мы должны сделать + = 1 на отрезке [max(0, idx - m + 1), idx] в нашем массиве v. Значит, чтобы ответить на запрос, мы должны поддержать структуру данных которая могла бы восстановить заданные значения в массиве v в на тот момент, когда все песни имели качество ≥ q. Кроме этого, она должна использовать мало памяти. В итоге ответ на запрос очевидно равен m - max(vi), lj ≤ i ≤ rj.
. Очевидно, когда мы добавляем новую песню позиции idx в рассмотрение, мы должны сделать + = 1 на отрезке [max(0, idx - m + 1), idx] в нашем массиве v. Значит, чтобы ответить на запрос, мы должны поддержать структуру данных которая могла бы восстановить заданные значения в массиве v в на тот момент, когда все песни имели качество ≥ q. Кроме этого, она должна использовать мало памяти. В итоге ответ на запрос очевидно равен m - max(vi), lj ≤ i ≤ rj.
Каждые  добавлений песен сохраним три величины: значение первого элемента в блоке позиций, максимум значения массива v на блоке, и дополнительно не более
добавлений песен сохраним три величины: значение первого элемента в блоке позиций, максимум значения массива v на блоке, и дополнительно не более  обновлений, которые пришли в текущем блоке обновлений, но не покрывали полностью заданный блок. Используя эти значения нужно аккуратно восстановить нужную информацию о массиве v и ответить на запрос.
обновлений, которые пришли в текущем блоке обновлений, но не покрывали полностью заданный блок. Используя эти значения нужно аккуратно восстановить нужную информацию о массиве v и ответить на запрос.
Авторское решение: 11035739









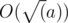 . Кроме того, можно ускорить работу этой функции, достаточно просто насчитать массив маленьких простых чисел. В таком решении очень важно не забыть, что каждый раз пересчитывать красоту чисел не нужно. Достаточно завести
. Кроме того, можно ускорить работу этой функции, достаточно просто насчитать массив маленьких простых чисел. В таком решении очень важно не забыть, что каждый раз пересчитывать красоту чисел не нужно. Достаточно завести 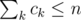 . Хорошо. Посчитаем динамическое программирование:
. Хорошо. Посчитаем динамическое программирование: 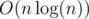 памяти, и построить можно за время
памяти, и построить можно за время  по времени /
по времени / 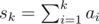 ;
;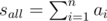 ;
;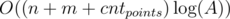 .
.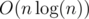
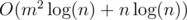 .
.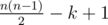 ребер.
ребер. . До остальных окружностей расстояние посчитать нетрудно: слева у нас
. До остальных окружностей расстояние посчитать нетрудно: слева у нас 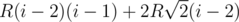 . Аналогичная ситуация справа.
. Аналогичная ситуация справа. 
 . Тогда
. Тогда 


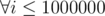 . Далее будем перебирать, сколько раз встретится цифра
. Далее будем перебирать, сколько раз встретится цифра 
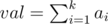 .
. 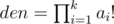 , это просто доказать, используя то факт, что
, это просто доказать, используя то факт, что 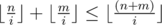 . Так же,
. Так же, 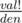 — мультиномиальный коэффициент. Итак, ответ не превосходит
— мультиномиальный коэффициент. Итак, ответ не превосходит 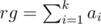 .
.
