I have no school right now, and there's no tutorials on Tree Isomorphism on Codeforces, so I decided to write one :).
What is a tree isomorphism?
Maybe you recognize the word isomorphic: in the context of abstract algebra when two objects are effectively the same, but are labelled differently. We can extend this to trees as well: two trees are isomorphic if they are the same, but may have different node labels. For example,
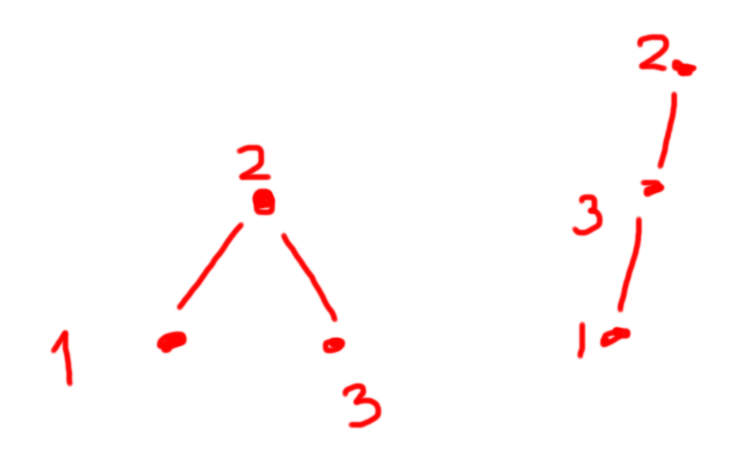 are isomorphic because we can relabel the nodes. If you want a more rigorous definition, then two trees $$$T_1 = (V_1, E_1)$$$ and $$$T_2 = (V_2, E_2)$$$ are isomorphic iff there exists a $$$\phi$$$ for which $$$\phi(E_1) = E_2$$$ and a $$$\phi^{-1}$$$ for which $$$\phi^{-1} (E_2) = E_1$$$.
are isomorphic because we can relabel the nodes. If you want a more rigorous definition, then two trees $$$T_1 = (V_1, E_1)$$$ and $$$T_2 = (V_2, E_2)$$$ are isomorphic iff there exists a $$$\phi$$$ for which $$$\phi(E_1) = E_2$$$ and a $$$\phi^{-1}$$$ for which $$$\phi^{-1} (E_2) = E_1$$$.
Does a tree being unrooted really matter?
No, not in the meaningful sense. We can transform our original problem of checking if two trees are isomorphic into checking if two rooted trees are isomorphic easily. How? We can find the centroids of our first tree and our centroids of our second tree, and then root them at their centroids. So now, we have transformed our unrooted case into a rooted case.





