I admit that AGC061C is too hard for me, and I don't even understand its official editorial. Today I see a Luogu blog with a very clear idea on this problem. I learned a lot from it, and I would like to share it to you now. The writer of this blog is possibly Little09, but I am not quite sure.

Part1: Problem Statement and Constraints

There are $$$N$$$ customers named $$$1$$$, ..., $$$N$$$ visiting a shop. Customer $$$i$$$ arrives at time $$$A_i$$$ and leaves at time $$$B_i$$$ The queue order is first in first out, so $$$A_i$$$ and $$$B_i$$$ are both increasing. Additionally, all $$$A_i$$$ and $$$B_i$$$ are pairwise distinct.

At the entrance, there's a list of visitors to put their names in. Each customer will write down their name next in the list exactly once, either when they arrive or when they leave. How many different orders of names can there be in the end? Find the count modulo $$$998244353$$$.

Constraints:

$$$\cdot 1 \leq N \leq 500000$$$.

$$$\cdot 1 \leq A_i \leq B_i \leq 2N$$$.

$$$\cdot A_i < A_{i+1}\,(1 \leq i \leq N-1)$$$.

$$$\cdot B_i < B_{i+1}\,(1 \leq i \leq N-1)$$$.

$$$\cdot A_i \neq B_j \,(i \neq j)$$$

$$$\cdot \text{All values in the input are integers}$$$.

Part2: Idea in the blog

Consider two dynamic programming tables named $$$f$$$ and $$$g$$$ ($$$dp$$$ in the original blog). The blog computes $$$f,\,g$$$ in the reverse order. Formally,

$$$f(i) (1 \leq i \leq n)$$$: The number of permutations when we have already considered persons $$$i,\,i+1,\,...,\,n$$$.

$$$g(i) (1 \leq i \leq n)$$$: The number of permutations when we have already considered persons $$$i,\,i+1,\,...,\,n$$$, and the person $$$i$$$ is forced to sign her (or his) name on $$$B_i$$$.

The blog defines $$$c(i)$$$ as:

$$$c(i) := max\{j|A_j < B_i\}$$$. (1)

Obviously $$$i \in \{j|A_j < B_i\}$$$ and $$$c(i) \geq i$$$.

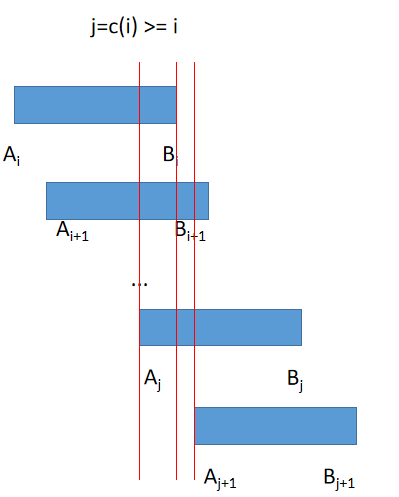
First, we consider $$$f(i)$$$. If $$$i$$$ signs on $$$A_i$$$, then no matter when $$$i+1,\,i+2,\,...\,n$$$ sign their name, $$$i$$$ is always placed in front of them. It is a bijection, given a permutation $$$p$$$ of $$$[i+1,\,i+2\,...\,n]$$$, just add $$$i$$$ in front of $$$p$$$. The number of distinct permutations when $$$i$$$ signs on $$$A_i$$$ is just $$$f(i+1)$$$. If $$$i$$$ signs on $$$B_i$$$, then $$$i$$$ must not be placed the first, otherwise it is overlapped with a situation where $$$i$$$ signs on $$$A_i$$$. Now we consider the number of permutations that $$$i$$$ is placed the first among $$$\{i,\,i+1,\,...,\,n\}$$$. In this case ($$$i$$$ is the first), $$$x \in \{i+1,\,i+2\,...,\,c(i)\}$$$ should all sign on $$$B_x$$$ because $$$A_x < B_i$$$ (according to the definition of $$$c$$$ in Eq.(1)), and the choices of $$$x \in \{c(i)+1,\,...,\,n\}$$$ are not important. The number of the permutations that $$$i$$$ signs on $$$B_i$$$ and $$$i$$$ is placed the first among $$$\{i,\,i+1,\,...,\,n\}$$$ is $$$g(c(i))$$$, because $$$c(i)$$$ must chooses $$$B_{c(i)}$$$ and $$$\{c(i)+1,\,j+2\,...,\,n\}$$$ can choose freely. Therefore, the situation where $$$i$$$ signed on $$$B_i$$$ contributes $$$g(i) - g(c(i))$$$ to $$$f(i)$$$. $$$f(i)$$$ depends on $$$g$$$:

$$$f(i) = f(i+1) + g(i) - g(c(i))$$$. (2)

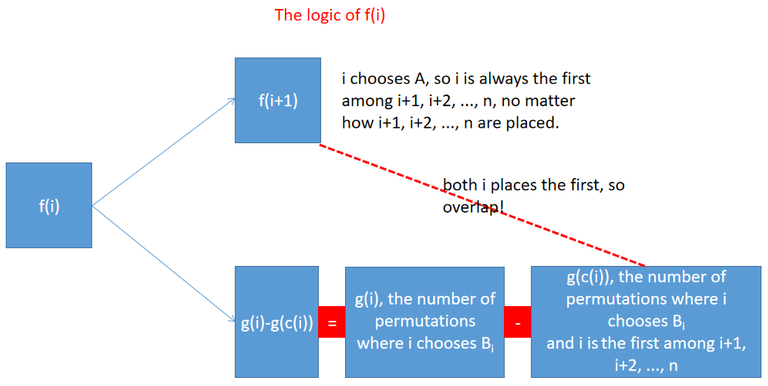
Second, we consider $$$g(i)$$$. To count $$$g(i)$$$, an important idea is to divide it into non-overlapping cases. The blog consider

$$$P_j$$$ := The set of permutations where $$$j$$$ is the least integer among $$$\{i+1,\,i+2\,...,\,c(i)\}$$$ such that $$$j$$$ chooses $$$B_j$$$. In other words, $$$i$$$ chooses $$$B_i$$$, $$$\{i+1,\,i+2\,...,\,j-1\}$$$ all choose $$$A$$$, and $$$j$$$ chooses $$$B_j$$$. Also, we should not forget $$$P_{c(i)+1}$$$, because $$$\{i+1,\,i+2\,...,\,c(i)\}$$$ might all choose $$$A$$$!

(1)Do these $$$P_j$$$ (including $$$P_{c(i)+1}$$$) overlap? No! Because the permutations in $$$P_j$$$ has a unique prefix: $$$[i+1\,i+2\,...,\,j-1]$$$.

(2)Do these $$$P_j$$$ cover all situations? Yes, this is obvious.

(3)How to calculate the size of $$$P_j$$$, i.e., $$$|P_j|$$$? For $$$j \leq c(i)$$$, since the prefix is fixed ($$$[i+1\,i+2\,...,\,j-1]$$$ mentioned in (1)), there is a bijection from the set $$$g(j)$$$ to $$$P_j$$$ by adding the fixed prefix to the element in $$$g(j)$$$. So the size of $$$|P_j|$$$ is just $$$g(j)$$$. For $$$j=c(i)+1$$$, $$$|P_j|=f(c(i)+1)$$$ because all $$$\{i+1,\,i+2\,...,\,c(i)\}$$$ have to choose $$$A$$$.

Therefore,

$$$g(i) = \sum\limits_{j=i+1}^{c(i)} g(j) + f(c(i)+1)$$$ (3)

Finally, although we consider $$$f$$$ first, we should calculate $$$g$$$ first because $$$f$$$ depends on $$$g$$$.

Part3: Implementation details

(1) You can use two pointers to calculate $$$c$$$.

(2) To make the computation of $$$g$$$ faster, you can use the prefix sum trick.

(3) In the original blog Little09 calculates from $$$n$$$ to $$$1$$$. You can also calculate from $$$1$$$ to $$$n$$$. Symmetrically, you should define $$$c(i)$$$ as $$$min\{j|B_j > A_i\}$$$, and define $$$g(i)$$$ as "The number of permutations when we have already considered persons $$$1,\,2,\,...,\,i-1$$$, and the person $$$i$$$ is forced to sign her (or his) name on $$$A_i$$$". Here is my implementation that calculates from $$$1$$$ to $$$n$$$.

Part4: What I have learned

(1) The most important idea in counting is dividing into non-overlapping sets whose unions are the whole set. Besides, the counting of each set should be much simpler.

(2) The most important thing of dp is defining states.

(3) Bijections are really important in combinatorics. For example, the Dyck path.

(4) Achieving (1) and (2) requires high IQ and talent. For example, the definition of $$$f$$$ in the blog is normal, while the definition of $$$g$$$ is genius!

Part4: The last

If you have any questions, please don't hesitate to ask me. It is beneficial for both of us. For you, I might resolve your confusion. For me, I can check whether I make a typo in the blog or not and whether I really understand this blog or not.